Задание 1.73 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1.73 учебника 2023-2024 (стр. 23):
Турист шел 2 ч по равнине, 1,5 ч поднимался в гору и 2,5 ч спускался с горы. Скорость туриста на равнине в 1,5 раза больше скорости при подъеме в гору, а скорость спуска с горы в 2 раза больше скорости при подъеме в гору. Найдите скорость туриста при подъеме в гору, если его средняя скорость на всем пути 4,75 км/ч.
№1.73 учебника 2021-2022 (стр. 22):
Постройте биссектрису:
а) прямого угла;
б) развернутого угла.
Подсказка
№1.73 учебника 2023-2024 (стр. 23):
Вспомните:
- Как найти среднюю скорость движения.
- Что называют уравнением, его корни.
- Задачи на движение.
- Сложение десятичных дробей.
- Умножение десятичных дробей.
- Деление десятичных дробей.
№1.73 учебника 2021-2022 (стр. 22):
Ответ
№1.73 учебника 2023-2024 (стр. 23):

Средняя скорость - 4,75 км/ч.
1) 1,5 + 3
+ 3 + 5
+ 5 = 9,5
= 9,5 (км) - весь пройденный путь.
(км) - весь пройденный путь.
2) 1,5 + 2 + 2,5 = 6 (ч) - время в пути.
3) 9,5 : 6 = 4,75
: 6 = 4,75
9,5 = 4,75 • 6
= 4,75 • 6
9,5 = 28,5
= 28,5
 = 28,5 : 9,5
= 28,5 : 9,5
 = 285 : 95
= 285 : 95
 = 3 (км/ч)
= 3 (км/ч)
| × | 4 | 7 | 5 |
| 6 | |||
| 2 | 8 | 5 | 0 |
Ответ: скорость туриста при подъеме в гору равна 3 км/ч.
Пояснения:
Решаем задачу с помощью уравнения.
Пусть  км/ч скорость туриста при подъеме в гору. Скорость туриста на равнине в 1,5 раза больше скорости при подъеме в гору, а скорость спуска с горы в 2 раза больше скорости при подъеме в гору. Значит, скорость туриста на равнине 1,5
км/ч скорость туриста при подъеме в гору. Скорость туриста на равнине в 1,5 раза больше скорости при подъеме в гору, а скорость спуска с горы в 2 раза больше скорости при подъеме в гору. Значит, скорость туриста на равнине 1,5 км/ч, а скорость спуска с горы - 2
км/ч, а скорость спуска с горы - 2 км/ч.
км/ч.
Чтобы найти расстояние, нужно скорость движения умножить на время.
Турист 1,5 ч поднимался в гору со скоростью  км/ч, значит, путь в гору равен: 1,5
км/ч, значит, путь в гору равен: 1,5 км.
км.
Турист шел 2 ч по равнине со скоростью 1,5 км/ч, значит, путь по равнине равен:
км/ч, значит, путь по равнине равен:
2 • 1,5 км = 3
км = 3 км.
км.
Турист 2,5 ч спускался с горы со скоростью 2 км/ч, значит, путь с горы равен:
км/ч, значит, путь с горы равен:
2,5 • 2 км = 5
км = 5 км.
км.
Тогда весь путь, пройденный туристом равен:
1,5 + 3
+ 3 + 5
+ 5 = 9,5
= 9,5 (км).
(км).
А все время в пути:
1,5 + 2 + 2,5 = 6 (ч).
Чтобы найти среднюю скорость движения, нужно весь пройденный путь разделить на все время движения.
Известно, что весь пройденный туристом путь 9,5 км, время, затраченное на этот путь 6 ч, а средняя скорость движения туриста 4,75 км/ч, значит, можем составить следующее уравнение:
км, время, затраченное на этот путь 6 ч, а средняя скорость движения туриста 4,75 км/ч, значит, можем составить следующее уравнение:
9,5 : 6 = 4,75.
: 6 = 4,75.
Сначала решаем полученное уравнение относительно деления, то есть находим неизвестное делимое. Чтобы найти неизвестное делимое, нужно, частное умножить на делитель, тогда:
9,5 = 4,75 • 6,
= 4,75 • 6,
9,5 = 28,5.
= 28,5.
Теперь решаем уравнение относительно умножения, то есть находим неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
 = 28,5 : 9,5,
= 28,5 : 9,5,
 = 285 : 95,
= 285 : 95,
 = 3.
= 3.
Учитывая обозначения, введенные выше, скорость туриста при подъеме в гору равна 3 км/ч.
№1.73 учебника 2021-2022 (стр. 22):
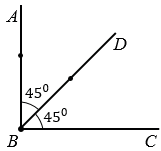
а) Прямой угол - 900.
900 : 2 = 450.

Луч ВD - биссектриса 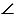 АВС = 900.
АВС = 900.
б) Развернутый угол - 1800.
1800 : 2 = 900.

Луч NP - биссектриса 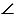 MNK = 1800.
MNK = 1800.
Пояснения:
Для того чтобы начертить угол с заданной градусной мерой, необходимо совместить начало луча, который определяет одну из сторон угла, с центром транспортира, так, чтобы этот луч прошел через нулевое деление шкалы транспортира, найти на шкале транспортира нужную градусную меру и провести через это значение вторую сторону угла.
а) Прямой угол равен 900. Биссектриса - это луч, который делит угол пополам. Тогда биссектриса прямого угла разделит его на два угла по 450 каждый, так как 900 : 2 = 450.
Построим прямой угол АВС и проведем биссектрису этого угла - луч ВD.
Чтобы построить 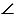 АВС = 900, чертим луч ВС и прикладываем центр транспортира к точке В, так, чтобы луч ВС прошел через нулевое деление на внутренней шкале транспортира и находим на внутренней шкале транспортира значения 900 и 450, ставим напротив них точки.
АВС = 900, чертим луч ВС и прикладываем центр транспортира к точке В, так, чтобы луч ВС прошел через нулевое деление на внутренней шкале транспортира и находим на внутренней шкале транспортира значения 900 и 450, ставим напротив них точки.

Чертим лучи с началом в точке В, которые пройдут через отмеченные точки, получаем 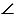 АВС = 900 и биссектрису угла АВС - луч ВD.
АВС = 900 и биссектрису угла АВС - луч ВD.
б) Развернутый угол равен 1800. Биссектриса - это луч, который делит угол пополам. Тогда биссектриса развернутого угла разделит его на два угла по 900 каждый, так как 1800 : 2 = 900.
Построим развернутый угол МNK и проведем биссектрису этого угла - луч NP.
Чтобы построить  MNK = 1800, нужно провести прямую МK и отметить на ней точку N.
MNK = 1800, нужно провести прямую МK и отметить на ней точку N.

Чтобы провести биссектрису развернутого угла МNK, прикладываем центр транспортира к точке N, так, чтобы луч NK прошел через нулевое деление на внутренней шкале транспортира и находим на внутренней шкале транспортира значение 900, ставим напротив него точку.

Чертим луч с началом в точке N, который пройдет через отмеченную точку, получаем  МNK = 1800 и биссектрису угла MNK - луч NP.
МNK = 1800 и биссектрису угла MNK - луч NP.

Вернуться к содержанию учебника