Задание 2.583 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 114

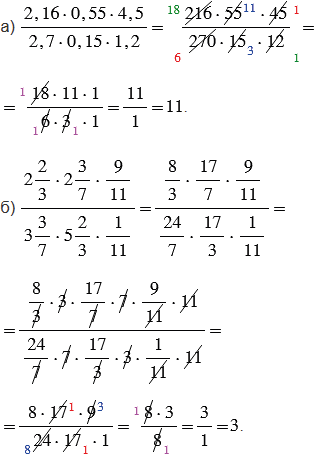
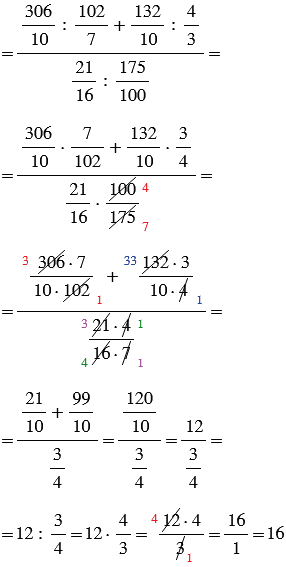
Пояснения:

Дробным выражением называют частное двух чисел или выражений, в котором знак деления обозначен чертой.

Выражение, стоящее над чертой, называют числителем, а выражение, стоящее под чертой - знаменателем дробного выражения. Числителем и знаменателем дробного выражения могут быть любые числа, а также числовые или буквенные выражения.

Чтобы найти значение дробного выражения, сначала выполняют действия в числителе, а затем действия в знаменателе. Последним выполняется действие деления: выражение в числителе делится на выражение в знаменателе.

Действиями первой ступени называют сложение и вычитание чисел, а действиями второй ступени - умножение и деление чисел.

При вычислении значений выражений в числителе и знаменателе дробного выражения порядок выполнения действий определяют следующие правила:

1. Если выражение содержит только действия одной ступени и в нем нет скобок, то действия выполняют по порядку слева направо.

2. Если в выражении нет скобок, то сначала выполняют действия второй ступени, потом - действия первой ступени.

3. Если в выражении есть скобки есть скобки, то сначала выполняют действия в скобках (учитывая правила 1 и 2).

В пункте а), чтобы получить в числителе и в знаменателе дробного выражения натуральные числа, перенесем в них запятую вправо в каждом множителе на равное количество знаков, то есть так, чтобы общее количество знаков, на которые перенесена запятая в числителе и знаменателе дробного выражения было одинаковым, затем выполняем сокращение. При переносе запятой учитываем то, что у десятичной дроби на конце можно дописывать сколько угодно нулей.

В пункте б) в числителе и в знаменателе дробных выражений сначала преобразуем смешанные числа в неправильные дроби, а затем получаем из них натуральные числа, для этого умножаем числитель и знаменатель дробного выражения на произведение чисел 3, 7 и 11.

В пунктах в) и г) отдельно выполняем вычисления в числителе и отдельно в знаменателе по правилам вычислений с обыкновенными дробями, затем делим результат вычислений в числите на результат вычислений в знаменателе.

Правила, по которым выполнены вычисления, смотри в подсказке.