Задание 1.125 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1.125 учебника 2023-2024 (стр. 31):
Пограничный пес Мухтар взял след и начал догонять нарушителя границы, когда между ними было 2,7 км, и догнал его через 0,18 ч. Найдите скорость Мухтара, если скорость нарушителя была в 3,5 раза меньше его скорости.
№1.125 учебника 2021-2022 (стр. 29):
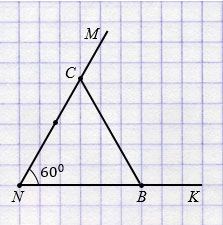
а) Постройте угол MNK, градусная мера которого равна 600. На сторонах угла отложите равные отрезки NB и NC и соедините отрезком точки В и С.
б) Измерьте стороны и углы треугольника CNB и сравните его стороны и углы.
в) Найдите сумму углов и периметр треугольника наиболее удобным способом.
Подсказка
№1.125 учебника 2023-2024 (стр. 31):
Вспомните:
- Задачи на движение.
- Деление десятичных дробей.
- Что называют уравнением, его корни.
- Умножение десятичных дробей.
- Вычитание десятичных дробей.
№1.125 учебника 2021-2022 (стр. 29):
Вспомните:
- Что называют углом.
- Градусная мера угла.
- Что называют треугольником, его периметр.
- Сложение чисел.
- Умножение чисел.
Ответ
№1.125 учебника 2023-2024 (стр. 31):
1) 2,7 : 0,18 = 270 : 18 = 15 (км/ч) - скорость сближения.
| - | 2 | 7 | 0 | 1 | 8 | |||||||||
| 1 | 8 | 1 | 5 | |||||||||||
| - | 9 | 0 | ||||||||||||
| 9 | 0 | |||||||||||||
| 0 |
2) Пусть  км/ч скорость нарушителя, тогда скорость Мухтара 3,5
км/ч скорость нарушителя, тогда скорость Мухтара 3,5 км/ч. Скорость сближения 15 км/ч.
км/ч. Скорость сближения 15 км/ч.
Составим уравнение:
3,5 -
-  = 15
= 15
2,5 = 15
= 15
 = 15 : 2,5
= 15 : 2,5
 = 150 : 25
= 150 : 25
 = 6 (км/ч) - скорость нарушителя.
= 6 (км/ч) - скорость нарушителя.
3) 3,5 = 3,5 • 6 = 21 (км/ч) - скорость Мухтара.
= 3,5 • 6 = 21 (км/ч) - скорость Мухтара.
| × | 3 | 5 |
| 6 | ||
| 2 | 1 | 0 |
Ответ: 21 км/ч скорость Мухтара.
Пояснения:
Чтобы найти скорость, нужно расстояние разделить на время.
Пограничный пес Мухтар взял след и начал догонять нарушителя границы, когда между ними было 2,7 км, и догнал его через 0,18 ч. Значит, скорость сближения Мухтара и нарушителя равна:
2,7 : 0,18 = 270 : 18 = 15 (км/ч).
Далее решаем задачу с помощью уравнения.
Пусть  км/ч скорость нарушителя. Скорость нарушителя была в 3,5 раза меньше скорости Мухтара, то есть скорость Мухтара в 3 раза больше скорости нарушителя, тогда скорость Мухтара 3,5
км/ч скорость нарушителя. Скорость нарушителя была в 3,5 раза меньше скорости Мухтара, то есть скорость Мухтара в 3 раза больше скорости нарушителя, тогда скорость Мухтара 3,5 км/ч. Скорость сближения Мухтара и нарушителя 15 км/ч. Следовательно, можем составить следующее уравнение:
км/ч. Скорость сближения Мухтара и нарушителя 15 км/ч. Следовательно, можем составить следующее уравнение:
3,5 -
-  = 15.
= 15.
Применяя в левой части уравнения распределительное свойство умножения относительно вычитания, получим:
(3,5 - 1) = 15 или, выполнив вычитание в скобках, 2,5
= 15 или, выполнив вычитание в скобках, 2,5 = 15.
= 15.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
 = 15 : 2,5,
= 15 : 2,5,
 = 150 : 25,
= 150 : 25,
 = 6.
= 6.
Учитывая обозначения введенные нами выше, скорость нарушителя равна 6 км/ч, а скорость Мухтара:
3,5 = 3,5 • 6 = 21 (км/ч).
= 3,5 • 6 = 21 (км/ч).
№1.125 учебника 2021-2022 (стр. 29):
а)  MNK = 600.
MNK = 600.
б) NB = NC = DC = 3 см.
 N =
N =  В =
В =  С = 600.
С = 600.
в) Сумма углов треугольника СNB:
600 • 3 = 1800.
Периметр треугольника СNB:
3 • 3 = 9 (см).
Ответ: сумма углов - 1800,
периметр - 9 см.
Пояснения:
а) Для того чтобы начертить угол с заданной градусной мерой, необходимо совместить начало луча, который определяет одну из сторон угла, с центром транспортира, так, чтобы этот луч прошел через нулевое деление шкалы транспортира, найти на шкале транспортира нужную градусную меру и провести через это значение вторую сторону угла.
Построим  MNK = 600. Чертим луч NK.
MNK = 600. Чертим луч NK.

Прикладываем центр транспортира к точке N так, чтобы луч NK прошел через нулевое деление на внутренней шкале транспортира. Находим на внутренней шкале транспортира значение 600, ставим напротив него точку.

Чертим луч NM, который пройдет через отмеченную точку, получаем
 MNK = 600.
MNK = 600.
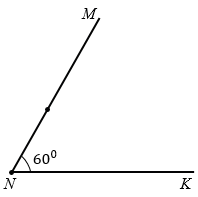
На луче NK откладываем отрезок NB = 3 см, а на луче NM откладываем отрезок NC = 3 см. Соединяем отрезком точки В и С.
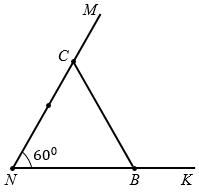
б) С помощью линейки измеряем стороны треугольника СNB, получаем:
NB = NC = DC = 3 см.
С помощью транспортира измеряем углы треугольника СNB, получаем:
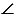 N =
N = 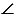 В =
В = 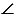 С = 600.
С = 600.
в) Так как в треугольнике СNB все углы равны, сумму углов можно заменить умножением градусной меры одного угла на 3, тогда сумма углов треугольника СNB равна:
600 • 3 = 1800.
Периметр треугольника равен сумме длин всех его сторон. Так как в треугольнике СNB все стороны равны, сумму сторон можно заменить умножением длины одной стороны на 3, тогда периметр треугольника СNB равен:
3 • 3 = 9 (см).
Вернуться к содержанию учебника