Задание 496 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№496 учебника 2013-2022 (стр. 133):
Основание D высоты СD треугольника АВС лежит на стороне АВ, причем АD = ВС. Найдите АС, если АВ = 3, а СD = 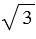 .
.
№496 учебника 2023-2024 (стр. 130):
Постройте параллелограмм: а) по двум смежным сторонам и углу между ними; б) по двум диагоналям и углу между ними; в) по двум смежным сторонам и соединяющей их концы диагонали.
Подсказка
№496 учебника 2013-2022 (стр. 133):
Вспомните:
- Какая фигура называется треугольником.
- Что такое высота треугольника.
- Теорему Пифагора.
№496 учебника 2023-2024 (стр. 130):
Вспомните:
- Какая фигура называется параллелограммом.
- Что такое диагональ многоугольника, какие его стороны называются смежными.
- Признаки параллелограмма.
- Как построить отрезок, равный данному.
- Как построить угол, равный данному.
- Как построить середину отрезка.
Ответ
№496 учебника 2013-2022 (стр. 133):



№496 учебника 2023-2024 (стр. 130):
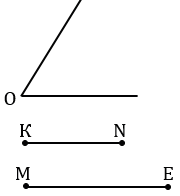
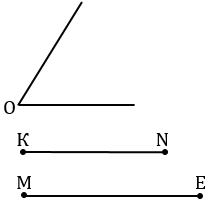
а) Дано: отрезки МЕ и КN, 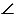 О.
О.
Построить: параллелограмм АВСD так, что АB = МЕ и ВС = KN, 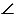 В =
В = 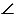 О.
О.
Построение:
Доказательство:
1. По построению ВС = МЕ и АD = МЕ,  ВС = АD.
ВС = АD.
2. По построению АВ = КN и СD = КN,  АВ = СD.
АВ = СD.
3. ВС = АD, АВ = СD, 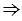 АВСD - параллелограмм (по признаку параллелограмма) такой, что АB = МЕ и ВС = KN,
АВСD - параллелограмм (по признаку параллелограмма) такой, что АB = МЕ и ВС = KN, 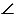 В =
В = 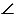 О (по построению).
О (по построению).
б) Дано: отрезки МЕ и КN, 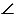 О.
О.
Построить: параллелограмм АВСD так, что АС = KN и ВD = ME, АС 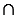 ВD = R,
ВD = R,  СRВ =
СRВ =  О.
О.
Построение:
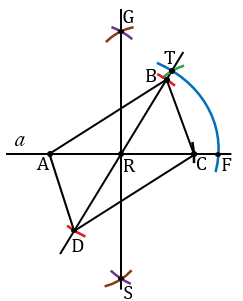
Доказательство:
АС и ВD - диагонали АВСD, AR = RC, т.к. по построению R - середина АС, DR = RВ - радиусы окружности с центром в точке R, 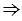 АВСD - параллелограмм. При этом АС = KN и ВD = ME, АС
АВСD - параллелограмм. При этом АС = KN и ВD = ME, АС 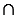 ВD = R,
ВD = R, 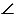 СRВ =
СRВ = 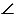 О,
О, 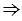 АВСD - искомый параллелограмм.
АВСD - искомый параллелограмм.
в) решение данного пункта приведено в учебнике на страницах 106-107.
Пояснения:
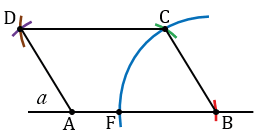
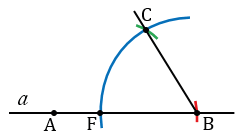
а) Строим два отрезка КN и МЕ, а также угол О.

Строим прямую 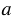 и отмечаем на ней точку А.
и отмечаем на ней точку А.
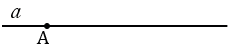
С помощью циркуля измеряем отрезок МЕ и строим окружность с центром в точке А радиуса МЕ (всю окружность строить необязательно, смотри выделенное красным цветом), точку пересечения данной окружности с прямой 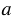 обозначаем буквой В.
обозначаем буквой В.
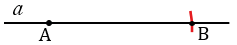
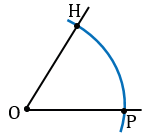
Далее строим угол В, равный углу О. Для этого строим окружность произвольного радиуса с центром в вершине угла О (всю окружность строить необязательно, смотри выделенное синим цветом). Точки пересечения данной окружности со сторонами угла О обозначаем буквами P и H.
Затем, строим окружность радиуса ОР с центром в точке В (всю окружность строить необязательно, смотри выделенное синим цветом),точку пересечения данной окружности с прямой 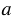 обозначаем буквой F. Измеряем с помощью циркуля расстояние РН и строим окружность радиуса РН с центром в точке F (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения окружностей с центрами в точках В и F обозначаем буквой С. Проводим прямую ВС.
обозначаем буквой F. Измеряем с помощью циркуля расстояние РН и строим окружность радиуса РН с центром в точке F (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения окружностей с центрами в точках В и F обозначаем буквой С. Проводим прямую ВС.
Теперь строим две окружности с центрами в точках А и С радиусами КN и МЕ соответственно (полностью окружности строить необязательно, смотри выделенное фиолетовым и коричневым цветом). Точку пересечения данных окружностей обозначаем буквой D. Соединяем точки А и D, С и D, получаем четырехугольник АВСD.

Докажем, что четырехугольник АВСD - искомый параллелограмм.
По построению ВС = МЕ и АD = МЕ, значит, ВС = АD.
По построению АВ = КN и СD = КN, значит, АВ = СD.
Итак, ВС = АD, АВ = СD, следовательно, четырехугольник АВСD - параллелограмм по признаку параллелограмма, который говорит о том, что если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм. При это по построению АB = МЕ и ВС = KN,  В =
В =  О, следовательно, параллелограмм АВСD - искомый.
О, следовательно, параллелограмм АВСD - искомый.
б) Строим два отрезка КN и МЕ, а также угол О.

Строим прямую  и отмечаем на ней точку А.
и отмечаем на ней точку А.
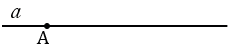
С помощью циркуля измеряем отрезок KN и строим окружность с центром в точке А радиуса KN (всю окружность строить необязательно, смотри выделенное красным цветом), точку пересечения данной окружности с прямой  обозначаем буквой С.
обозначаем буквой С.
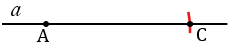
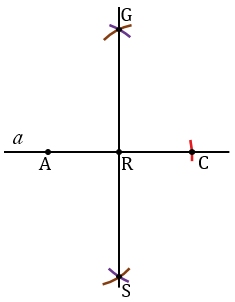
Затем находим середину отрезка АС. Для этого строим окружности радиуса АС с центрами в точках А и С (полностью окружности строить необязательно, смотри выделенное фиолетовым и коричневым цветом). Точки пересечения данных окружностей обозначаем буквами G и S. Проводим прямую через точки G и S, точку пересечения прямой GS с прямой  обозначаем буквой R.
обозначаем буквой R.
Теперь построим угол СRT, равный углу О. Для этого строим окружность произвольного радиуса с центром в вершине угла О (всю окружность строить необязательно, смотри выделенное синим цветом). Точки пересечения данной окружности со сторонами угла О обозначаем буквами P и H.

Затем, строим окружность радиуса ОР с центром в точке R (всю окружность строить необязательно, смотри выделенное синим цветом), точку пересечения данной окружности с прямой 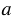 обозначаем буквой F. Измеряем с помощью циркуля расстояние РН и строим окружность радиуса РН с центром в точке F (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения окружностей с центрами в точках В и F обозначаем буквой T. Проводим прямую RT.
обозначаем буквой F. Измеряем с помощью циркуля расстояние РН и строим окружность радиуса РН с центром в точке F (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения окружностей с центрами в точках В и F обозначаем буквой T. Проводим прямую RT.
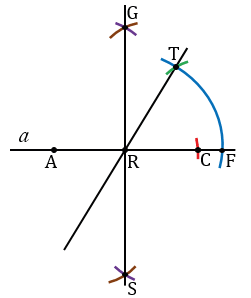
Затем находим середину отрезка ME. Для этого строим окружности радиуса ME с центрами в точках M и E (полностью окружности строить необязательно, смотри выделенное фиолетовым и коричневым цветом). Точки пересечения данных окружностей обозначаем буквами Y и X. Проводим прямую через точки Y и X, точку пересечения прямой YX с отрезком МЕ обозначаем буквой Z.
С помощью циркуля измеряем отрезок ZE и строим окружность с центром в точке R радиуса ZE (всю окружность строить необязательно, смотри выделенное красным цветом). Точки пересечения данной окружности с прямой RT обозначаем буквами В и D.
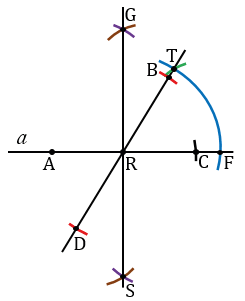
Соединяем точки А и В, В и С, С и D, А и D, получаем четырехугольник АВСD.

Докажем, что четырехугольник АВСD - искомый параллелограмм.
АС и ВD - диагонали, т.к. соединяют противоположные вершины четырехугольника АВСD, AR = RC, т.к. по построению R - середина АС, DR = RВ - радиусы окружности с центром в точке R, следовательно, по признаку параллелограмма, который говорит о том, что если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм, получим, что АВСD - параллелограмм. При этом АС = KN и ВD = ME, АС  ВD = R,
ВD = R,  СRВ =
СRВ =  О, значит, АВСD - искомый параллелограмм.
О, значит, АВСD - искомый параллелограмм.
Вернуться к содержанию учебника