Задание 500 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№500 учебника 2013-2022 (стр. 134):
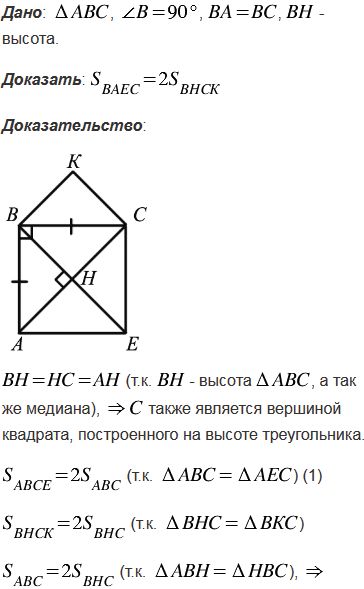
Докажите, что площадь квадрата , построенного на катете равнобедренного прямоугольного треугольника, вдвое больше площади квадрата, построенного на высоте, проведённой к гипотенузе.
№500 учебника 2023-2024 (стр. 131):
Постройте равнобедренную трапеция АВСD:
а) по основанию АD, углу А и боковой стороне АВ;
б) по основанию ВС, боковой стороне АВ и диагонали ВD.
Подсказка
№500 учебника 2013-2022 (стр. 134):
Вспомните:
- Что такое треугольник.
- Какой треугольник называется прямоугольным.
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Что такое квадрат.
- Что такое площадь.
№500 учебника 2023-2024 (стр. 131):
Вспомните:
- Какая трапеция называется равнобедренной.
- Как построить отрезок, равный данному.
- Как построить угол, равный данному.
- Что такое диагональ трапеции.
Ответ
№500 учебника 2013-2022 (стр. 134):


№500 учебника 2023-2024 (стр. 131):
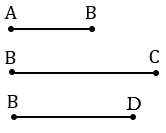
а) Дано: ВС - основание, АВ - боковая сторона, ВD - диагональ.
Построить: трапецию АВСD.
Построение:
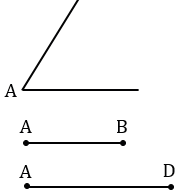
б) Дано: 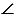 A, AD - основание, АВ - боковая сторона.
A, AD - основание, АВ - боковая сторона.
Построить: трапецию АВСD.
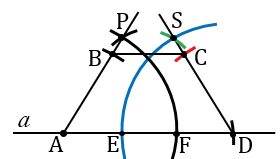
Построение:
Пояснения:
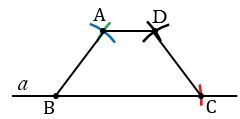
а) Чертим два отрезка АВ, АD и угол А.

Строим прямую 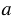 и отмечаем на ней точку А. С помощью циркуля измеряем отрезок АD и строим окружность с центром в точке А радиуса АD (всю окружность строить необязательно, смотри выделенное красным цветом), точку пересечения данной окружности с прямой
и отмечаем на ней точку А. С помощью циркуля измеряем отрезок АD и строим окружность с центром в точке А радиуса АD (всю окружность строить необязательно, смотри выделенное красным цветом), точку пересечения данной окружности с прямой 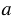 обозначаем буквой D.
обозначаем буквой D.
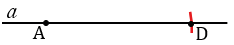
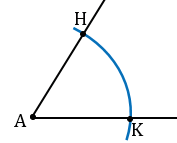
Далее от луча АD откладываем угол, равный углу А. Для этого строим окружность произвольного радиуса с центром в вершине угла А (всю окружность строить необязательно, смотри выделенное синим цветом). Точки пересечения данной окружности со сторонами угла А обозначаем буквами K и H.
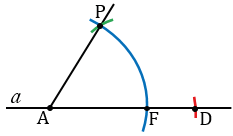
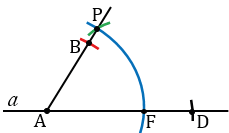
Затем, строим окружность с центром в точке A радиуса AK (всю окружность строить необязательно, смотри выделенное синим цветом), точку пересечения данной окружности с прямой 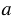 обозначаем буквой F. Измеряем с помощью циркуля расстояние KН и строим окружность радиуса KН с центром в точке F (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения окружностей с центрами в точках A и F обозначаем буквой P. Проводим прямую AP.
обозначаем буквой F. Измеряем с помощью циркуля расстояние KН и строим окружность радиуса KН с центром в точке F (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения окружностей с центрами в точках A и F обозначаем буквой P. Проводим прямую AP.
Теперь на луче АP откладываем отрезок, равный AB. Для этого строим окружность с центром в точке А радиуса AB (всю окружность строить необязательно, смотри выделенное красным цветом). Точку пересечения данной окружности с лучом АP обозначаем буквой B.
У равнобедренной трапеции боковые стороны равны и углы при основании равны, поэтому строим окружность с центром в точке D радиуса AK (всю окружность строить необязательно, смотри выделенное синим цветом), точку пересечения данной окружности с прямой 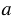 обозначаем буквой E. Измеряем с помощью циркуля расстояние KН и строим окружность радиуса KН с центром в точке E (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения окружностей с центрами в точках D и E обозначаем буквой S. Проводим прямую DS.
обозначаем буквой E. Измеряем с помощью циркуля расстояние KН и строим окружность радиуса KН с центром в точке E (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения окружностей с центрами в точках D и E обозначаем буквой S. Проводим прямую DS.
Теперь на луче DS откладываем отрезок, равный AB. Для этого строим окружность с центром в точке D радиуса AB (всю окружность строить необязательно, смотри выделенное красным цветом). Точку пересечения данной окружности с лучом DS обозначаем буквой C. Соединяем точки В и С, получаем четырехугольник АВСD, который является искомой равнобедренной трапецией по построению.

б) Чертим три отрезка АВ, ВС,ВD.

Строим прямую  и отмечаем на ней точку В. С помощью циркуля измеряем отрезок ВС и строим окружность с центром в точке В радиуса ВС (всю окружность строить необязательно, смотри выделенное красным цветом), точку пересечения данной окружности с прямой
и отмечаем на ней точку В. С помощью циркуля измеряем отрезок ВС и строим окружность с центром в точке В радиуса ВС (всю окружность строить необязательно, смотри выделенное красным цветом), точку пересечения данной окружности с прямой 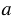 обозначаем буквой С.
обозначаем буквой С.
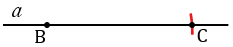
Далее строим окружность радиуса АВ с центром в точке С (всю окружность строить необязательно, смотри выделенное синим цветом) и окружность радиуса ВD c центром в точке В (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения данных окружностей обозначаем буквой D.
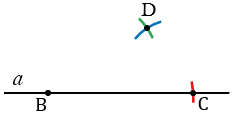
У равнобедренной трапеции равны боковые грани и равны диагонали, поэтому строим окружность радиуса АВ с центром в точке В (всю окружность строить необязательно, смотри выделенное синим цветом) и окружность радиуса ВD c центром в точке C (всю окружность строить необязательно, смотри выделенное зеленым цветом). Точку пересечения данных окружностей обозначаем буквой А.
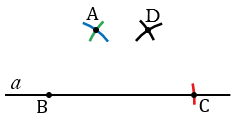
Теперь соединяем точки А и В, А и D, С и D, получаем четырехугольник АВСD, который является искомой равнобедренной трапецией по построению.

Вернуться к содержанию учебника