Страница 72. Повторение - ГДЗ Математика 3 класс. Петерсон. Учебник часть 3
Вернуться к содержанию учебника
Страница 69. Повторение Страница 70. Повторение Страница 71. Повторение Страница 72. Повторение Страница 73. Повторение Страница 74. Повторение Страница 75. Повторение
Вопрос
Задание № 42. Сравни выражения, где буквы обозначают натуральные числа:
m + 48  80 + m 80 + m |
36 : х  24 : х 24 : х |
60 - n  25 - n 25 - n |
b : 5  b : 3 b : 3 |
k - 18  k - 53 k - 53 |
(9 + c) • 4  9 + c • 4 9 + c • 4 |
a + a + a  2 • a 2 • a |
d • 6 - d  d • 5 d • 5 |
Подсказка
Повтори, что такое буквенные выражения и неравенства.
Ответ
Решение
| m + 48 < 80 + m | 36 : х > 24 : х |
| 60 - n > 25 - n | b : 5 < b : 3 |
| k - 18 > k - 53 | (9 + c) • 4 > 9 + c • 4 |
| a + a + a > 2 • a | d • 6 - d = d • 5 |
Пояснение
m + 48 < 80 + m - слагаемое m в суммах одинаковое, а слагаемое 48 первой суммы меньше, чем слагаемое 80 второй суммы. С увеличением слагаемых сумма увеличивается. Поэтому ставим знак "<".
60 - n > 25 - n - вычитаемые в разностях одинаковые, а уменьшаемое в первой разности больше, чем во второй. Чем больше уменьшаемое, тем больше разность. Значит, надо поставить знак "<".
k - 18 > k - 53 - уменьшаемые в разностях одинаковые, а вычитаемое в первой разности меньше, чем во второй. Чем больше вычитаемое, тем меньше разность. Следовательно, первая разность больше второй. Ставим знак "<".
a + a + a > 2 • a - слева три слагаемых, равных а, а справа - только два, так как по переместительному свойству умножения 2 • а = а • 2 = а + а. Значит, надо поставить знак "<".
36 : х > 24 : х - делитель в обоих выражениях одинаковый, а делимое слева больше, чем справа. Если делимое уменьшается, то и частное уменьшается, поэтому ставим знак ">".
b : 5 < b : 3 - делимое в данных выражениях одинаковое, а делитель слева больше, чем справа. Если делитель уменьшается, то частное увеличивается, поэтому надо поставить знак "<".
(9 + c) • 4 > 9 + c • 4 - в левой части равенства по распределительному свойству умножения произведение равно сумме 9 • 4 + с • 4. Выражение справа отличается тем, что у него первое слагаемое равно 9, а не 9 • 4, поэтому оно меньше. Значит, и вся сумма справа больше. Ставим знак ">".
d • 6 - d = d • 5 - слева имеется 6 - 1 = 5 слагаемых, равных d, и справа 5 таких слагаемых. Следовательно, при всех значениях d значения выражений равны. Ставим знак "=".
Вопрос
Задание № 43. Ворон живёт 60 лет, а овца - в 5 раз меньше ворона. Лошадь живёт на 4 года больше овцы, а хомяк - в 8 раз меньше лошади. Сколько лет живёт хомяк?
Подсказка
Повтори случаи табличного и внетабличного деления, а также что такое задача.
Ответ
Вопрос
Задание № 44. Четыре зайчишки-братишки пошли в поле за морковками. Каждый из них принёс домой по 45 морковок. За ужином съели 36 морковок, а остальные разложили поровну в 3 пакета. Сколько морковок в каждом пакете?
Ответ
Решение
1) 45 • 4 = 180 (м.) - принесли.
2) 180 - 36 = 144 (м.) - разложили.
3) 144 : 3 = 48 (м.)
| - | 1 | 4 | 4 | 3 | ||||||||||
| 1 | 2 | 4 | 8 | |||||||||||
| - | 2 | 4 | ||||||||||||
| 2 | 4 | |||||||||||||
| 0 |
Ответ: 48 морковок в каждом пакете.
Пояснение

Сколько морковок принесли?
1) 45 • 4 = 180 (м.)
Сколько морковок разложили?
2) 180 - 36 = 144 (м.)
Сколько морковок в каждом пакете?
3) 144 : 3 = 48 (м.)
4 зайчишки принесли по 45 морковок каждый. Вычислим, сколько морковок они принесли:
1) 45 • 4 = 180 (м.)
Принесли 180 морковок, за ужином съели 36 морковок, а остальные разложили по пакетам. Вычислим, сколько морковок разложили:
2) 180 - 36 = 144 (м.)
144 морковки разложили поровну в 3 пакета. Узнаем, сколько морковок в каждом пакете:
3) 144 : 3 = 48 (м.)
Вопрос
Задание № 45. В саду у Хрюши росла яблонька. Осенью он собрал урожай - 50 яблок. По 2 яблока Хрюша подарил 5 белочкам и по 3 яблока дал ёжикам. Сколько яблок у него ещё осталось?
Ответ
Вопрос
Задание № 46. Бежала Мышка по полю и нашла 6 колосков по 40 зёрен в каждом. Чтобы испечь пирог, ей нужно 30 зёрен. Сколько пирогов сможет испечь Мышка из найденных колосков?
Ответ
Решение
1) 40 • 6 = 240 (з.) - нашла.
2) 240 : 30 = 8 (п.)
Ответ: 8 пирогов может испечь Мышка из найденных колосков.
Пояснение
Сколько колосков нашла Мышка?
1) 40 • 6 = 240 (з.)
Сколько пирогов может испечь Мышка?
2) 240 : 30 = 8 (п.)
Мышка нашла 6 колосков по 40 зёрен в каждом. Вычислим, сколько колосков нашла Мышка:
1) 40 • 6 = 240 (з.)
Мышка нашла 240 колосков. Чтобы испечь пирог, ей нужно 30 зёрен. Вычислим, сколько пирогов может испечь Мышка:
2) 240 : 30 = 8 (п.)
Вопрос
Задача № 47. Белочка заготавливает грибы на зиму - каждый день одинаковое число грибов. За 5 дней она успела заготовить 40 грибов. Сколько грибов она сможет заготовить за неделю (7 дней)? За сколько дней она заготовит 200 грибов?
Ответ
Решение
1) 40 : 5 = 8 (гр.) - за 1 день.
2) 8 • 7 = 56 (гр.) - за неделю.
3) 200 : 8 = 25 (дн.)
Ответ: 56 грибов может заготовить за неделю, за 25 дней она заготовит 200 грибов.
Пояснение
Сколько грибов белочка заготавливает за 1 день?
1) 40 : 5 = 8 (гр.)
Сколько грибов она сможет заготовить за неделю?
2) 8 • 7 = 56 (гр.)
За сколько дней она заготовит 200 грибов?
3) 200 : 8 = 25 (дн.)
Белочка за 5 дней успела заготовить 40 грибов. Вычислим, сколько грибов белочка заготавливает за 1 день:
1) 40 : 5 = 8 (гр.)
Белочка за 1 день заготавливает 56 грибов. Вычислим, сколько грибов она сможет заготовить за неделю:
2) 8 • 7 = 56 (гр.)
Белочка за 1 день заготавливает 8 грибов. Узнаем, за сколько дней она заготовит 200 грибов:
3) 200 : 8 = 25 (дн.)
Вопрос
Задание № 48. Буратино во сне собирал с деревьев урожай золотых монет. С первого дерева он собрал 312 монет, со второго - в 2 раза меньше, чем с первого, а с третьего - на 28 монет больше, чем со второго. Из них 652 монеты он потратил на подарки для папы Карло. Сколько монет осталось у Буратино в его прекрасном сне?
Подсказка
Ответ
Решение
1) 312 : 2 = 156 (м.) - со второго дерева.
| - | 3 | 1 | 2 | 2 | |||||||||||
| 2 | 1 | 5 | 6 | ||||||||||||
| - | 1 | 1 | |||||||||||||
| 1 | 0 | ||||||||||||||
| - | 1 | 2 | |||||||||||||
| 1 | 2 | ||||||||||||||
| 0 |
2) 156 + 28 = 184 (м.) - с третьего дерева.
3) 312 + 156 + 128 = 468 (м.) - с трёх деревьев.
| + | 3 | 1 | 2 |
| 1 | 5 | 6 | |
| 1 | 8 | 4 | |
| 6 | 5 | 2 |
4) 652 - 652 = 0 (м.)
Ответ: в прекрасном сне у Буратино не осталось монет.
Пояснение

Сколько монет собрали со второго дерева?
1) 312 : 2 = 156 (м.)
Сколько монет собрали с третьего дерева?
2) 156 + 28 = 184 (м.)
Сколько монет собрали с трёх деревьев?
3) 312 + 156 + 128 = 468 (м.)
Сколько монет осталось у Буратино в его прекрасном сне?
4) 652 - 652 = 0 (м.)
С первого дерево Буратино собрал 312 монет, со второго - в 2 раза меньше, чем с первого. Вычислим, сколько монет собрали со второго дерева:
1) 312 : 2 = 156 (м.)
Со второго дерева собрали 156 монет. Вычислим, сколько монет собрали с третьего дерева:
2) 156 + 28 = 184 (м.)
С первого дерева он собрал 312 монет, со второго - 156 монет, а с третьего 184 монеты. Вычислим, сколько монет собрали с трёх деревьев:
3) 312 + 156 + 128 = 468 (м.)
С трёх деревьев собрали 468 монет. Узнаем, сколько монет осталось у Буратино в его прекрасном сне:
4) 652 - 652 = 0 (м.)
Вопрос
Задание № 49. Винтик и Шпунтик подтянулись вместе 36 раз. Шпунтик подтянулся на 14 раз меньше Винтика. Сколько раз подтянулся каждый из них?
Ответ
Решение
1) (36 - 14) : 2 = 11 (р.) - подтянулся Шпунтик.
2) 11 + 14 = 25 (р.)
Ответ: 11 раз подтянулся Шпунтик, 25 раз подтянулся Винтик.
Пояснение
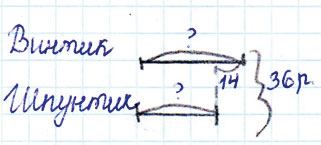
Сколько раз подтянулся Шпунтик?
1) (36 - 14) : 2 = 11 (р.)
Сколько раз подтянулся Винтик?
2) 11 + 14 = 25 (р.)
Винтик и Шпунтик подтянулись вместе 36 раз. Шпунтик подтянулся на 14 раз меньше Винтика. То есть, убрав разницу, получится, что у каждого количество раз одинаковое. Вычислим, сколько раз подтянулся Шпунтик:
1) (36 - 14) : 2 = 11 (р.)
Шпунтик подтянулся 11 раз. Это на 14 раз меньше Винтика. Узнаем, сколько раз подтянулся Винтик:
2) 11 + 14 = 25 (р.)
Вернуться к содержанию учебника

