Страница 60. Урок 26 - ГДЗ Математика 3 класс. Петерсон. Учебник часть 3
Вернуться к содержанию учебника
Страница 56. Урок 25 Страница 57. Урок 25 Страница 59. Урок 26 Страница 60. Урок 26 Страница 61. Урок 27 Страница 62. Урок 27 Страница 63. Урок 28
Вопрос
Задание № 2. В магазин привезли 120 кг яблок, груш - в 2 раза меньше, чем яблок, а персиков - на 12 кг больше, чем груш. Сколько всего килограммов яблок, груш и персиков привезли в магазин?
Подсказка
Повтори, как делить круглые числа.
Ответ
Решение
1) 120 : 2 = 60 (кг) - груш.
2) 60 + 12 = 72 (кг) - персиков.
3) 120 + 60 + 72 = 252 (кг)
Ответ: 252 кг яблок, груш и персиков привезли в магазин.
Пояснение
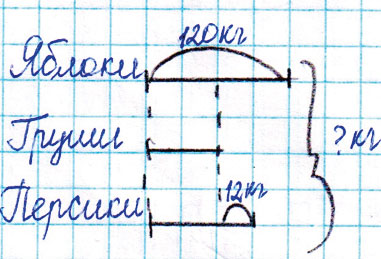
Сколько килограммов груш привезли?
1) 120 : 2 = 60 (кг)
Сколько килограммов персиков привезли?
2) 60 + 12 = 72 (кг)
Сколько всего килограммов яблок, груш и персиков привезли в магазин?
3) 120 + 60 + 72 = 252 (кг)
В магазин привезли 120 кг яблок, груш - в 2 раза меньше. Вычислим, сколько килограммов груш привезли:
1) 120 : 2 = 60 (кг)
Привезли 60 кг груш, а персиков - на 12 кг больше. Вычислим, сколько килограммов персиков привезли:
2) 60 + 12 = 72 (кг)
В магазин привезли 120 кг яблок, 60 кг груш и 72 кг персиков. Узнаем, сколько всего килограммов яблок, груш и персиков привезли в магазин:
3) 120 + 60 + 72 = 252 (кг)
Вопрос
Задание № 3. На шоссе стоят четыре восьмиэтажных жилых дома. На каждом этаже каждого из этих домов по 9 квартир. Из всех этих квартир 128 однокомнатных, 96 двухкомнатных, а остальные - трёхкомнатные. Сколько всего трёхкомнатных квартир в этих домах?
Подсказка
Повтори случаи табличного и внетабличного умножения.
Ответ
Решение
1) 9 • 8 = 72 (кв.) - в каждом доме.
2) 72 • 4 = 288 (кв.) - всего.
3) 288 - 128 - 96 = 64 (кв.)
Ответ: 64 трёхкомнатных квартир в этих домах.
Пояснение

Сколько квартир в каждом доме?
1) 9 • 8 = 72 (кв.)
Сколько квартир всего в этих домах?
2) 72 • 4 = 288 (кв.)
Сколько всего трёхкомнатных квартир в этих домах?
3) 288 - 128 - 96 = 64 (кв.)
В восьмиэтажном доме на каждом этаже по 9 квартир. Вычислим, сколько квартир в каждом доме:
1) 9 • 8 = 72 (кв.)
В каждом из четырёх домов по 72 квартиры. Вычислим, сколько квартир всего в этих домах:
2) 72 • 4 = 288 (кв.)
Всего 288 квартир. Из них 128 однокомнатных квартир, 96 двухкомнатных, а остальные - трёхкомнатные. Узнаем, сколько всего трёхкомнатных квартир в этих домах:
3) 288 - 128 - 96 = 64 (кв.)
Вопрос
Задание № 4. Расстояние между Москвой и Минском 720 км. Автомобиль ехал из Москвы со скоростью 80 км/ч, а на обратном пути - увеличил скорость на 10 км/ч. Сколько времени затратил автомобиль на весь путь из Москвы в Минск и обратно?
Подсказка
Повтори взаимосвязь между скоростью, временем и расстоянием.
Ответ
Решение
1) 80 + 10 = 90 (км/ч) - скорость на обратном пути.
2) 720 : 80 = 9 (ч) - из Москвы в Минск.
3) 720 : 90 = 8 (ч) - из Минска в Москву.
4) 9 + 8 = 17 (ч)
Ответ: 17 ч затратил автомобиль на весь путь из Москвы в Минск и обратно.
Пояснение
| s | v | t | ||
| В Минск | 720 км | 80 км/ч | ? ч | 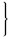 ? ч ? ч |
| В Москву | 720 км | (80 + 10) км/ч | ? ч | |
Какова скорость на обратном пути?
1) 80 + 10 = 90 (км/ч)
Сколько времени было затрачено на путь из Москвы в Минск?
2) 720 : 80 = 9 (ч)
Сколько времени было затрачено на путь из Минска в Москву?
3) 720 : 90 = 8 (ч)
Сколько времени затратил автомобиль на весь путь из Москвы в Минск и обратно?
4) 9 + 8 = 17 (ч)
Автомобиль ехал из Москвы в Минск со скоростью 80 км/ч, а на обратном пути - увеличил скорость на 10 км/ч. Вычислим, какова скорость на обратном пути:
1) 80 + 10 = 90 (км/ч)
Автомобиль ехал из Москвы в Минск 720 км со скоростью 80 км/ч. Вычислим, сколько времени было затрачено на путь из Москвы в Минск:
2) 720 : 80 = 9 (ч)
Автомобиль ехал из Минска в Москву 720 км со скоростью 90 км/ч. Вычислим, сколько времени было затрачено на путь из Минска в Москву?
3) 720 : 90 = 8 (ч)
Автомобиль ехал из Москвы в Минск 9 ч, а из Минска в Москву - 8 ч. Узнаем, сколько времени затратил автомобиль на весь путь из Москвы в Минск и обратно:
4) 9 + 8 = 17 (ч)
Вопрос
Задание № 5. В первом куске 12 м ткани, а во втором - 8 м такой же ткани. Первый кусок дороже второго на 320 руб. Сколько рублей стоит каждый из этих кусков ткани?
Подсказка
Ответ
Решение
1) 12 - 8 = 4 (м) - больше в первом куске.
2) 320 : 4 = 80 (руб.) - цена одного метра ткани.
3) 80 • 12 = 960 (руб.)
4) 80 • 8 = 640 (руб.)
Ответ: первый кусок стоит 960 руб., а второй кусок - 640 руб.
Пояснение
| C | a | n | |
| I | ? руб. | одинаковая | 12 м |
| II | ? руб. | 8 м | |
| I - II | 320 руб. | (12 - 8) м |
На сколько метров больше в первом куске, чем во втором?
1) 12 - 8 = 4 (м)
Какова цена одного метра ткани?
2) 320 : 4 = 80 (руб.)
Сколько стоит первый кусок ткани?
3) 80 • 12 = 960 (руб.)
Сколько стоит второй кусок ткани?
4) 80 • 8 = 640 (руб.)
В первом куске 12 м ткни, во втором - 8 м. Вычислим, на сколько метров больше в первом куске, чем во втором:
1) 12 - 8 = 4 (м)
4 м ткани стоят 320 руб. Вычислим, какова цена одного метра ткани:
2) 320 : 4 = 80 (руб.)
Один метр ткани стоит 80 руб. Вычислим, сколько стоит первый кусок ткани:
3) 80 • 12 = 960 (руб.)
Один метр ткани стоит 80 руб. Вычислим, сколько стоит второй кусок ткани:
4) 80 • 8 = 640 (руб.)
Вопрос
Задание № 6. Сумма площадей двух прямоугольников, имеющих одинаковую длину, равна 220 дм2. Ширина первого прямоугольника 4 дм, а ширина второго - на 3 дм больше, чем первого. Чему равна длина этих прямоугольников?
Подсказка
Повтори единицу длины - дециметр, а также как найти площадь прямоугольника.
Ответ
Решение
1) 4 + 3 = 7 (дм) - ширина II прямоугольника.
2) 4 + 7 = 11 (дм) - сума ширины I и II прямоугольников.
3) 220 : 11 = 20 (дм)
Ответ: длина прямоугольников 20 дм.
Пояснение
Чтобы найти общую длину прямоугольников, можно их площадь разделить на сумму ширины первого и второго прямоугольника. Ширина первого прямоугольника известна - 4 дм, а ширину второго можем найти, увеличив 4 дм на 3 дм.
| S | a | b | |
| I | ? дм2 | одинаковая | 4 дм |
| II | ? дм2 | (4 + 3) дм | |
| I + II | 220 дм2 | (4 + (4 + 3)) дм |
Вопрос
Задание № 7. Выполни действия:
| а) 374 • 75 | в) 850 • 39800 | д) 7263000 : 90 |
| б) 908 • 132 | г) 4620 • 5040 | е) 24040000 : 800 |
Ответ
Решение
а)
|
в)
|
д)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
б)
|
г)
|
е)
|
Пояснение
а) Пишу: 374 • 75.
Умножу первый множитель на число единиц:
374 • 5 = 1870.
Получу первое неполное произведение: 1870.
Умножу первый множитель на число десятков:
374 • 7 = 2618.
Получу второе неполное произведение: 2618 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 28050. Это произведение чисел 374 и 75.
б) Пишу: 132 • 908.
Умножу первый множитель на число единиц:
132 • 8 = 1056.
Получу первое неполное произведение: 1056.
В десятках второго множителя - ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
132 • 9 = 1188.
Получу второе неполное произведение: 1188 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 119856. Это произведение чисел 132 и 908.
в) Пишу: 39800 • 850.
При умножении круглых чисел в столбик числа записывают и умножают, не смотря на нули. Затем к результату приписывают справа столько нулей, сколько в обоих множителях вместе.
Умножу первый множитель на число единиц:
398 • 5 = 1990.
Получу первое неполное произведение: 1990.
Умножу первый множитель на число десятков:
398 • 8 = 3184.
Получу второе неполное произведение: 3184 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 33830000. Это произведение чисел 39800 и 850.
г) Пишу: 4620 • 5040.
При умножении круглых чисел в столбик числа записывают и умножают, не смотря на нули. Затем к результату приписывают справа столько нулей, сколько в обоих множителях вместе.
Умножу первый множитель на число единиц:
462 • 4 = 1848.
Получу первое неполное произведение: 1848.
В десятках второго множителя - ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
462 • 5 = 2310.
Получу второе неполное произведение: 2310 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 23284800. Это произведение чисел 4620 и 5040.
д) При делении круглых чисел углом (без остатка) можно отбросить в делимом и делителе поровну нулей.
Пишу: 726300 : 9.
7 сот. тыс. нельзя разделить на 9 так, чтобы в частном получились сотни тысяч.
Делю десятки тысяч.
72 тыс. - это первое неполное делимое, значит в записи частного будет 5 цифр.
Разделю 72 на 9, получу 8 - столько десятков тысяч будет в частном.
Умножу 8 на 9, получу 72 - столько десятков тысяч разделили.
Вычту 72 из 72, получу 0 - десятки тысяч разделили все.
Делю единицы тысяч.
6 ед. тыс. нельзя разделить на 9 так, чтобы в частном получились единицы тысяч. Пишу в частное 0.
Делю сотни.
Разделю 63 на 9, получу 7 - столько сотен будет в частном.
Умножу 9 на 7, получу 63 - столько сотен разделили.
Вычту 63 из 63, получу 0 - сотни разделили все.
Десятков 0, единиц 0, поэтому записываю нули в частное.
Читаю ответ: 80700.
е) При делении круглых чисел углом (без остатка) можно отбросить в делимом и делителе поровну нулей.
Пишу: 240400 : 8.
2 сот. тыс. нельзя разделить на 8 так, чтобы в частном получились сотни тысяч.
Делю десятки тысяч.
24 тыс. - это первое неполное делимое, значит в записи частного будет 5 цифр.
Разделю 24 на 8, получу 3 - столько десятков тысяч будет в частном.
Умножу 8 на 3, получу 24 - столько десятков тысяч разделили.
Вычту 24 из 24, получу 0 - десятки тысяч разделили все.
Делю единицы тысяч.
0 ед. тыс., поэтому пишу в частное 0.
Делю сотни.
4 сот. нельзя разделить на 8 так, чтобы в частном получились сотни. Пишу в частное 0.
Делю десятки.
Разделю 40 на 8, получу 5 - столько десятков будет в частном.
Умножу 5 на 8, получу 40 - столько десятков разделили.
Вычту 63 из 63, получу 0 - десятки разделили все.
Единиц 0, поэтому пишу в частное 0.
Читаю ответ: 30050.
Вопрос
Задание № 8. Составь программу действий и вычисли:
| а) (18560 - 17915) • (4235 : 5 + 9535) |
| б) (600300 - 728 • 604) : 4 • (1700 • 390) |
Подсказка
Ответ
Вопрос
Задание № 9. Игра "Распутай клубок"
Расшифруй записи и вычисли указанные произведения.
Подсказка
Повтори алгоритм письменного умножения многозначных чисел.
Ответ
Решение
3600 • 660 = 2310000
5604 • 473 = 2650692
767 • 504 = 386568
Пояснение
|
|
|
Вернуться к содержанию учебника



