Страница 75 - ГДЗ Математика 3 класс. Моро, Бантова. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
1. Восстанови пропущенные цифры и числа.
1 • 7 = • 7 =  1 1 |
 8 • 8 •  = =  4 4 |
2 • 3 = • 3 =  5 5 |
9 : :  = =  4 4 |
 9 • 9 •  = =  7 7 |
7 : :  = 1 = 1 |
Найди все решения.
Подсказка
Повтори, что такое равенства, случаи табличного и внетабличного умножения, а также внетабличного деления.
Ответ
Решение
| 13 • 7 = 91 |
19 • 3 = 57 или 29 • 3 = 87 |
98 : 7 = 14 |
| 25 • 3 = 75 |
18 • 3 = 54 или 28 • 3 = 84 |
77 : 7 = 11 |
Пояснение
1 • 7 =
• 7 =  1
1
Какое число нужно умножить на 7, чтобы получилось в единицах 1? Это число 3, так как 3 • 7 = 21. Подставим его в первый множитель и узнаем второе недостающее число:
13 • 7 = 91
13 • 7 = (10 + 3) • 7 = 10 • 7 + 3 • 7 = 70 + 21 = 91
2 • 3 =
• 3 =  5
5
Какое число нужно умножить на 3, чтобы в единицах получилось 5? Это число 5, так как 5 • 3 = 15. Подставим его в первый множитель и узнаем второе недостающее число:
25 • 3 = 75
25 • 3 = (20 + 5) • 3 = 20 • 3 + 5 • 3 = 60 + 15 = 75
 9 •
9 •  =
=  7
7
На какое число нужно умножить 9, чтобы в единицах получилось 7? Это число 3, так как 9 • 3 = 27. Подставим его на место второго множителя и узнаем остальные пропущенные числа:
 9 • 3 =
9 • 3 =  7
7
1) Подставим в первый множитель цифру 1:
19 • 3 = (10 + 9) • 3 = 10 • 3 + 9 • 3 = 57
2) Подставим в первый множитель цифру 2:
29 • 3 = (20 + 9) • 3 = 20 • 3 + 9 • 3 = 87
3) Подставим в первый множитель цифру 3:
39 • 3 = (30 + 9) • 3 = 30 • 3 + 9 • 3 = 107.
В ответе по условию должно получиться двузначное число, поэтому нам подходят только варианты 1 и 2.
 8 •
8 •  =
=  4
4
На какое число нужно умножить 8, чтобы в единицах получилось 4? Это число 3, так как 8 • 3 = 24. Подставим его на место второго множителя и узнаем остальные пропущенные числа:
 8 • 3 =
8 • 3 =  4
4
1) Подставим в первый множитель цифру 1:
18 • 3 = (10 + 8) • 3 = 10 • 3 + 8 • 3 = 54
2) Подставим в первый множитель цифру 2:
28 • 3 = (20 + 8) • 3 = 20 • 3 + 8 • 3 = 84
3) Подставим в первый множитель цифру 3:
38 • 3 = (30 + 8) • 3 = 30 • 3 + 8 • 3 = 104
В ответе по условию должно получиться двузначное число, поэтому нам подходят только варианты 1 и 2.
9 :
:  =
=  4
4
1) Подставим в частное цифру 1. Подставим такой делитель, чтобы в искомом делимом было 9 десятков:
14 • 7 = (10 + 4) • 7 = 10 • 7 + 4 • 7 = 98
Значит, исходное равенство:
98 : 7 = 14
2) Подставим в частное цифру 2. Подставим такой делитель, чтобы в искомом делимом было 9 десятков:
24 • 4 = (20 + 4) • 4 = 20 • 4 + 4 • 4 = 96
Значит, исходное равенство:
96 : 4 = 24
3) Подставим в частное цифру 3. При подстановке любого делителя, нет числа с 9 десятками, которое давало бы 34 в ответе.
4) Подставим в частное цифру 4. При подстановке любого делителя, нет числа с 9 десятками, которое давало бы 44 в ответе.
Далее рассуждаем аналогично.
Также мы знаем, что при делении числа на 1, получается то же самое число, поэтому ещё возможно равенство:
94 : 1 = 94.
7 :
:  = 1
= 1
1) Подставим в частное цифру 1. Подставим такой делитель, чтобы в искомом делимом было 7 десятков:
11 • 7 = (10 + 1) • 7 = 10 • 7 + 1 • 7 = 77
Значит, исходное равенство:
77 : 7 = 11
2) Подставим в частное цифру 2. Подставим такой делитель, чтобы в искомом делимом было 7 десятков:
12 • 6 = (10 + 2) • 6 = 10 • 6 + 2 • 6 = 72
Значит, исходное равенство:
72 : 6 = 12
3) Подставим в частное цифру 3. Подставим такой делитель, чтобы в искомом делимом было 7 десятков:
13 • 6 = (10 + 3) • 6 = 10 • 6 + 3 • 6 = 78
Значит, исходное равенство:
78 : 6 = 13
4) Подставим в частное цифру 4. Подставим такой делитель, чтобы в искомом делимом было 7 десятков:
14 • 5 = (10 + 4) • 5 = 10 • 5 + 4 • 5 = 70
Значит, исходное равенство:
70 : 5 = 14
5) Подставим в частное цифру 5. Подставим такой делитель, чтобы в искомом делимом было 7 десятков:
15 • 5 = (10 + 5) • 5 = 10 • 5 + 5 • 5 = 75
Значит, исходное равенство:
75 : 5 = 15
6) Подставим в частное цифру 6. При подстановке любого делителя, нет числа с 7 десятками, которое давало бы 16 в ответе.
Далее рассуждаем аналогично.
Вопрос
2. Восстанови пропущенные цифры в делимом и пропущенные числа в остатке так, чтобы остаток был наибольшим из возможных для каждого делителя.
6 : 7 = 8 (ост.
: 7 = 8 (ост.  )
)
 9 : 6 = 9 (ост.
9 : 6 = 9 (ост.  )
)
8 : 9 = 9 (ост.
: 9 = 9 (ост.  )
)
 1 : 8 = 8 (ост.
1 : 8 = 8 (ост.  )
)
Подсказка
Ответ
Решение
| 62 : 7 = 8 (ост. 6) | 80 : 9 = 9 (ост. 8) |
| 59 : 6 = 9 (ост. 5) | 71 : 8 = 8 (ост. 7) |
Пояснение
1) Делитель - 7, значит остаток - 6.
Найдём делимое: 8 • 7 + 6 = 62.
Искомое равенство: 62 : 7 = 8 (ост. 6)
2) Делитель - 6, значит остаток - 5.
Найдём делимое: 9 • 6 + 5 = 59.
Искомое равенство: 59 : 6 = 9 (ост. 5)
3) Делитель - 9, значит остаток - 8.
Найдём делимое: 9 • 9 + 8 = 89.
Искомое равенство: 89 : 9 = 9 (ост. 8)
4) Делитель - 8, значит остаток - 7.
Найдём делимое: 8 • 8 + 7 = 71.
Искомое равенство: 71 : 8 = 8 (ост. 7)
Вопрос
3. Садовник рассадил 90 луковиц тюльпанов на 3 клумбы: большую, среднюю и маленькую. На среднюю клумбу он посадил в 2 раза больше луковиц, чем на маленькую, а на большую - столько же, сколько на маленькую и среднюю вместе. Сколько луковиц тюльпанов на каждой клумбе?
Подсказка
Ответ
Решение
1) 90 : 6 = 15 (л.) - на маленькую.
2) 15 • 2 = 30 (л.) - на среднюю.
3) 15 • 3 = 45 (л.) - на большую.
Ответ: 15 луковиц тюльпанов, 30 луковиц тюльпанов, 45 луковиц тюльпанов.
Пояснение
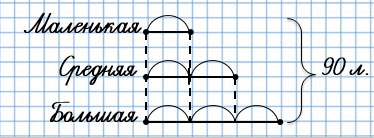
Обозначим маленькую клумбу отрезком. Поскольку на средней клумбе в 2 раза больше тюльпанов, то её мы обозначим двумя такими отрезками. Большая клумба - такая же, как маленькая и средняя вместе. То есть её мы можем обозначить тремя такими отрезками. Все клумбы вместе - это 6 маленьких отрезков. Узнаем, сколько луковиц тюльпанов на 1 маленьком отрезке:
1) 90 : 6 = 15 (л.)
Поскольку маленькая клумба - это и есть один отрезок, значит на ней всего 15 луковиц тюльпанов.
Средняя клумба - 2 маленьких отрезка, значит мы можем найти их количество следующим действием:
2) 15 • 2 = 30 (л.)
Количество луковиц тюльпанов на третьей клумбе мы можем найти двумя способами. Или использовать информацию, что большая клумба - 3 маленьких отрезка:
3) 15 • 3 = 45 (л.),
или сложить уже известное нам количество луковиц на маленькой и средней клумбах:
3) 30 + 15 = 45 (л.)
Теперь проверим, правильно ли мы рассуждали, сложив луковицы на всех клумбах:
15 + 30 + 45 = 45 + 45 = 90 (л.)
Общее количество луковиц совпало с данным в условии, значит задача решена верно.
Вопрос
4. Начерти ломаную из трёх звеньев так, чтобы её длина была равна 12 см, а второе звено было на 2 см длиннее первого и на столько же сантиметров короче третьего.
Подсказка
Повтори, что такое ломаная.
Ты можешь начертить другую ломаную, используя наши пояснения.
Ответ
Решение
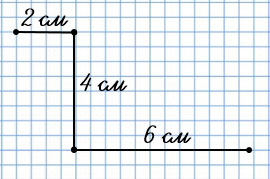
Пояснение
Мы знаем, что длина 2 звена - это длина 1 звена + 2 см (2 + 2 = 4 (см)), а длина третьего звена - это длина второго цвета + 2 см (4 + 2 = 6 (см)) или длина первого + 4 см (2 + 4 = 6 (см)).
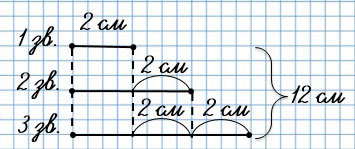
Найдём разницу в длинах между звеньями:
1) 2 + 2 + 2 = 6 (см)
Общая длина ломаной - 12 см. Вычтем из них разницу длин и найдём длину трёх маленьких отрезков:
2) 12 - 6 = 6 (см)
Найдём длину одного маленького отрезка. Это и будет длина 1 звена:
3) 6 : 3 = 2 (см)
Найдём длину 2 звена:
4) 2 + 2 = 4 (см)
Найдём длину 3 звена:
5) 2 + (2 + 2) = 2 + 4 = 6 (см)
Вопрос
5. 1) При делении одного и того же числа на 5 и на 9 получаются одинаковые частные, но при делении на 5 получается остаток 4, а деление на 9 выполняется без остатка. Какое число делили?
2) При делении одного и того же двузначного числа на 13 и на 14 получаются одинаковые частные, но при делении на 13 получается остаток 8, а при делении на 14 - остаток 4. Какое число делили?
Подсказка
Повтори случаи табличного и внетабличного деления, а также случаи деления с остатком.
Ответ
Решение
1) 9, так как
9 : 9 = 1 и 9 : 5 = 1 (ост. 4)
2) 60, так как
60 : 14 = 4 (ост. 4) и 60 : 13 = 4 (ост. 8)
Пояснение
1) Решаем путём подбора. Если деление на 9 выполняется без остатка, возьмём его за делитель. Первое число, которое делится без остатка на 9 - это 9.
9 : 9 = 1
Проверим то же число с делителем 5:
9 : 5 = 1 (ост. 4).
Полученные результаты соответствуют условию, поэтому искомое делимое - 9.
2) Решаем путём подбора. Возьмём за делитель число 14. Первое число, которое делится без остатка на 14 - это 14.
Прибавим к делимому данный в условии остаток:
14 + 4 = 18.
18 : 14 = 1 (ост. 4)
Проверим предполагаемое частное с другим данным делителем:
18 : 13 = 1 (ост. 5)
Нам требуется остаток 8, значит число 18 - не подходит.
Второе число, которое делится на 14 без остатка - 28.
Прибавим к делимому данный в условии остаток:
28 + 4 = 32
32 : 14 = 2 (ост. 4)
Проверим предполагаемое частное с другим данным делителем:
32 : 13 = 2 (ост. 6)
Нам требуется остаток 8, значит число 32 - не подходит.
Третье число, которое делится на 14 без остатка - 42.
Прибавим к делимому данный в условии остаток:
42 + 4 = 46
46 : 14 = 3 (ост. 4)
Проверим предполагаемое частное с другим данным делителем:
46 : 13 = 3 (ост. 7)
Нам требуется остаток 8, значит число 46 - не подходит.
Следующее число, которое делится на 14 без остатка - 56.
Прибавим к делимому данный в условии остаток:
56 + 4 = 60.
60 : 14 = 4 (ост. 4)
Проверим предполагаемое частное с другим данным делителем:
60 : 13 = 4 (ост. 8)
Полученные результаты соответствуют условию, поэтому искомое делимое - 60.
Вернуться к содержанию учебника