Задание 542 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Выберите год учебника
Вопрос
№542 учебника 2013-2022 (стр. 140):
В подобных треугольниках АВС и KMN стороны АВ и КМ, ВС и МN являются сходственными. Найдите стороны треугольника КМN, если АВ = 4 см, ВС = 5 см, СА = 7 см,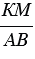 
= 2,1 см.
№542 учебника 2023-2024 (стр. 144):
Начертите квадрат и примите его за единицу измерения площадей. Далее начертите: а) квадрат, площадь которого выражается числом 4; б) прямоугольник, отличный от квадрата, площадь которого выражается числом 4; в) треугольник, площадь которого выражается числом 2.
Подсказка
№542 учебника 2013-2022 (стр. 140):
Вспомните:
- Какая фигура называется треугольником.
- Какие треугольники называются подобными.
- Какие отрезки называются пропорциональными.
№542 учебника 2023-2024 (стр. 144):
Вспомните:
- Что такое площадь многоугольника, ее свойства.
- Какая фигура называется квадратом.
- Какая фигура называется прямоугольником.
- Какая фигура называется треугольником.
Ответ
№542 учебника 2013-2022 (стр. 140):
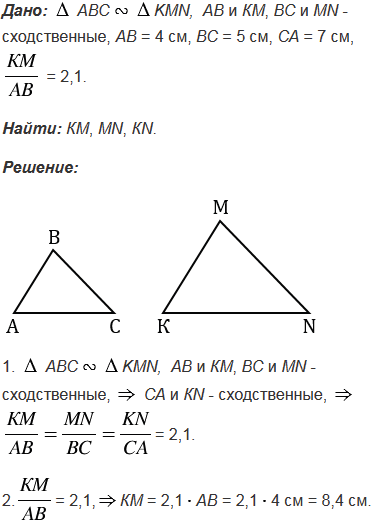
№542 учебника 2023-2024 (стр. 144):
а) 
б) 
в)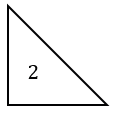 
Пояснения:
Чертим произвольный квадрат, площадь которого принимаем за 1.
а) Для того, чтобы построить квадрат, площадь которого выражается числом 4, нужно взять четыре квадрата с площадью 1 и составить из них квадрат, площадь которого и будет равна 4, т.к по свойству 20 площадей: если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
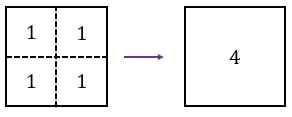
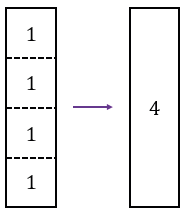
б) Для того, чтобы построить прямоугольник, отличный от квадрата, площадь которого выражается числом 4, нужно взять четыре квадрата с площадью 1 и составить из них прямоугольник. площадь которого и будет равна 4, т.к по свойству 20 площадей: если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
в) Для того, чтобы построить треугольник, площадь которого выражается числом 2, нужно взять четыре квадрата с площадью 1 и составить из них квадрат, площадь которого будет равна 4, затем разбить по одной из диагоналей этот квадрат на два треугольника, в результате чего, мы получим два треугольника с площадями 2, т.к. диагональ квадрата делит его на два равных треугольника, а по свойству 10 площадей: равные многоугольники имеют равные площади.
Вернуться к содержанию учебника