Задание 344 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Выберите год учебника
Вопрос
№344 учебника 2013-2022 (стр. 93):
В треугольнике АВС стороны АВ и АС не равны, отрезок АМ соединяет вершину А с произвольной точкой М стороны ВС. Докажите, что треугольники АМВ и АМС не равны друг другу.
№344 учебника 2023-2024 (стр. 103):
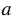касается окружности с центром О. Найдите расстояние от точки О до прямой 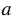, если диаметр окружности равен 14 см.Подсказка
№344 учебника 2013-2022 (стр. 93):
Вспомните:
- Какая фигура называется треугольником.
- Какие треугольники называются равными.
- Какой угол называется внешним углом треугольника.
№344 учебника 2023-2024 (стр. 103):
Вспомните:
- Теорему о касательной.
- Что называют расстоянием от точки до прямой.
Ответ
№344 учебника 2013-2022 (стр. 93):
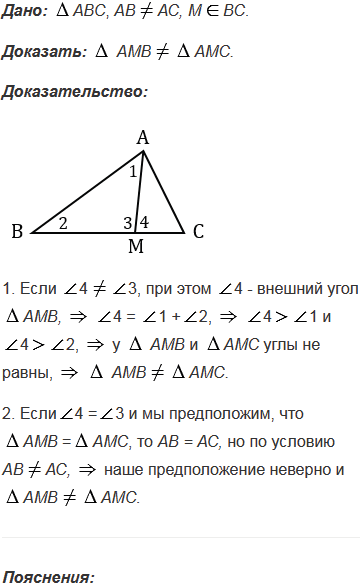
№344 учебника 2023-2024 (стр. 103):
Дано: окружность с центром О, d - ее диаметр, d = 14 см,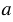 
- касательная.
Найти: расстояние от точки О до прямой .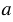
Решение:
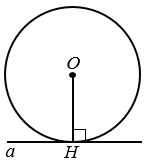
ОН - радиус, 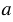- касательная, 
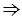ОН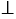 
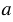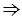, ОН - расстояние от точки О до прямой 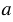и ОН = d : 2 = 14 : 2 = 7 (см).
Ответ: расстояние от точки О до прямой 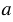7 см.
Пояснения:
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
ОН - радиус, 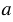- касательная, следовательно, ОН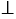 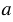, значит, ОН - расстояние от точки О до прямой 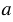, т.к. расстояние от точки до прямой - это длина перпендикуляра (т.е. наименьшее расстояние), проведенного из данной точки к данной прямой.
По условию диаметр окружности d = 14 см, а радиус окружности в 2 раза меньше диаметра, тогда расстояние от точки О до прямой :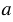
ОН = d : 2 = 14 : 2 = 7 (см).
Вернуться к содержанию учебника