Упражнение 1046 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(10x = 3b \)   \(/ : 10\)

\(x = \frac{3b}{10}\)

\(\frac{3b}{10} < 0\)  \(/\times 10\)

\(3b < 0\)   \(/ : 3\)

\(b < 0\)

Ответ: \(b \in (- \infty; 0)\).

б) \(x - 4 = b\)

\(x = b + 4\)

\(b + 4 < 0 \)

\(b < -4\)

Ответ: \(b \in (- \infty; -4)\).

в) \(3x - 1 = b + 2 \)

\(3x = b + 2 + 1 \)

\(3x = b + 3 \)  \(/ : 3\)

\(x = \frac{b + 3}{3}\)

\(\frac{b + 3}{3} < 0 \)  \(/ \times3\)

\(b + 3 < 0 \)

\(b < -3\)

Ответ: \(b \in (- \infty; -3)\).

г) \(3x - 3 = 5b - 2 \)

\(3x = 5b + 1 \)   \(/ : 3\)

\(x = \frac{5b + 1}{3}\)

\(\frac{5b + 1}{3} < 0\) \(/ \times3\)

\(5b + 1 < 0 \)

\(5b < -1 \)

\(b < -\frac{1}{5} \)

\(b < -0,2\)

Ответ: \(b \in (- \infty; -0,2)\).

Пояснения:

Основные правила.

- Сначала в каждом уравнении выражаем \(x\):

Если \(kx = m\), то \(x = \frac{m}{k}\) при \(k \ne 0.\)

- Чтобы уравнение имело отрицательный корень, найденное выражение для \(x\) должно удовлетворять условию \(x < 0\), то есть получается неравенство относительно \(b\), которое нужно решить.

При решении неравенств используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства разделить или умножить на одно и то же положительное число, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.

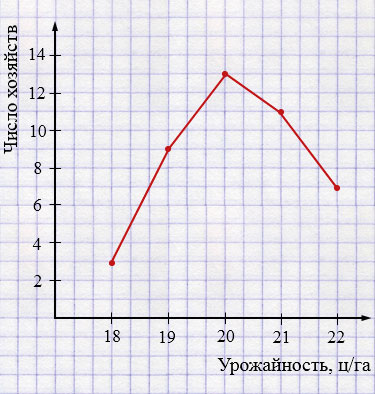
Пояснения:

Полигон распределения — это ломаная линия, показывающая, как изменяется частота (количество хозяйств) в зависимости от значения признака (урожайности).

Построение:

1. По горизонтальной оси откладывают значения урожайности.

2. По вертикальной оси откладывают число хозяйств.

3. В соответствии с данными из таблицы строят точки с координатами:

\((18; 3)\)

\((19; 9)\)

\((20; 13)\)

\((21; 11)\)

\((22; 7)\)

4. Эти точки нужно последовательно соединить отрезками.