Упражнение 937 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№937 учебника 2023-2025 (стр. 211):
Решите неравенство \(5x + 1 > 11\). Укажите три каких-нибудь решения этого неравенства.
№937 учебника 2013-2022 (стр. 209):
Найдите пересечение и объединение:
а) множества целых чисел и множества положительных чисел;
б) множества простых чисел и множества нечётных натуральных чисел.
Подсказка
№937 учебника 2023-2025 (стр. 211):
Вспомните:
№937 учебника 2013-2022 (стр. 209):
Вспомните:
Ответ
№937 учебника 2023-2025 (стр. 211):
\(5x + 1 > 11\)
\(5x > 11 - 1\)
\(5x > 10\) \(/ : 5\)
\(x > 2\).
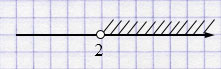
\((2; +\infty)\).
Ответ: \(x = 3\), \(x = 10\), \(x = 100\).
Пояснения:
При решении неравенства помним:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.
Если знак неравенства строгий (\(>\) или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.
Если знак неравенства нестрогий (\(\geq\) или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.
У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.
№937 учебника 2013-2022 (стр. 209):
а) Пересечением множества целых чисел и множества положительных чисел является множество натуральных чисел.
Объединением множества целых чисел и множества положительных чисел является множество целых отрицательных чисел, ноль и множество положительных чисел.
б) Пересечением множества простых чисел и множества нечётных натуральных чисел является множество простых чисел, кроме числа 2.
Объединением множества простых чисел и множества нечётных натуральных чисел является множество нечетных натуральных чисел и число 2.
Пояснения:
Пересечение \(\cap\) двух множеств — это множество чисел, которые принадлежат и первому, и второму промежутку одновременно.
Объединение \(\cup\) двух множеств — это множество чисел, которые принадлежат хотя бы одному из них.
Вернуться к содержанию учебника