Упражнение 881 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№881 учебника 2023-2025 (стр. 197):
Сложите почленно неравенства:
а) \(12 > -5\) и \(9 > 7\);
б) \(-2{,}5 < -0{,}7\) и \(-6{,}5 < -1{,}3\).
№881 учебника 2013-2022 (стр. 199):
Решите систему неравенств:
а) \(\begin{cases} 2x - 1 < 1,4 - x, \\ 3x - 2 > x - 4; \end{cases}\)
б) \(\begin{cases} 5x + 6 \leq x, \\ 3x + 12 \leq x + 17; \end{cases}\)
в) \(\begin{cases} 17x - 2 >12x - 1, \\ 3 - 9x < 1 - x; \end{cases}\)
г) \(\begin{cases} 25 - 6x \leq 4 + x, \\ 3x + 7,7 > 1 + 4x. \end{cases}\)
Подсказка
№881 учебника 2023-2025 (стр. 197):
Вспомните:
- Сложение числовых неравенств.
- Сложение рациональных чисел.
- Сложение десятичных дробей.
№881 учебника 2013-2022 (стр. 199):
Вспомните:
- Решение систем неравенств с одной переменной.
- Числовые промежутки.
- Решение неравенств с одной переменной.
- Деление и дроби.
- Деление десятичных дробей.
- Деление рациональных чисел.
- Сложение и вычитание десятичных дробей.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
Ответ
№881 учебника 2023-2025 (стр. 197):
а) \(12 > -5\) и \(9 > 7\);
\(12 + 9 > -5 + 7\)
\(21 > 2\)
б) \(-2{,}5 < -0{,}7\) и \(-6{,}5 < -1{,}3\)
\(-2{,}5 + (-6{,}5) < -0{,}7 + (-1{,}3)\)
\(-9 < -2\)
Пояснения:
Если почленно сложить верные неравенства одного знака, то получится верное неравенство:
- если \(a < b\) и \(c < d\), то
\(a + c < b + d\);
- если \(a > b\) и \(c > d\), то
\(a + c > b + d\).
№881 учебника 2013-2022 (стр. 199):
а) \(\begin{cases} 2x - 1 < 1,4 - x, \\ 3x - 2 > x - 4 \end{cases}\)
\(\begin{cases} 2x + x < 1,4 + 1, \\ 3x - x > -4 + 2 \end{cases}\)
\(\begin{cases} 3x < 2,4, / : 3 \\ 2x > -2 / : 2 \end{cases}\)
\(\begin{cases} x < 0,8, \\ x > -1 \end{cases}\)
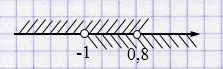
Ответ: \((-1; 0,8)\).
б) \(\begin{cases} 5x + 6 \leq x, \\ 3x + 12 \leq x + 17 \end{cases}\)
\(\begin{cases} 5x - x \leq -6, \\ 3x - x \leq 17 - 12 \end{cases}\)
\(\begin{cases} 4x \leq -6, / : 4 \\ 2x \leq 5 / : 2 \end{cases}\)
\(\begin{cases} x \leq -\frac{6}{4}, \\ x \leq \frac{5}{2} \end{cases}\)
\(\begin{cases} x \leq -1,5, \\ x \leq 2,5 \end{cases}\)

Ответ: \((- \infty; -1,5]\).
в) \(\begin{cases} 17x - 2 >12x - 1, \\ 3 - 9x < 1 - x \end{cases}\)
\(\begin{cases} 17x - 12x > -1 + 2, \\ -9x + x < 1 - 3 \end{cases}\)
\(\begin{cases} 5x > 1, / : 5 \\ -8x < -2 / : (-8) \end{cases}\)
\(\begin{cases} x > \frac15, \\ x > \frac28 \end{cases}\)
\(\begin{cases} x > 0,2, \\ x > \frac14 \end{cases}\)
\(\begin{cases} x > 0,2, \\ x > 0,25 \end{cases}\)

Ответ: \((0,25; +\infty)\).
г) \(\begin{cases} 25 - 6x \leq 4 + x, \\ 3x + 7,7 > 1 + 4x \end{cases}\)
\(\begin{cases} -6x - x \leq 4 - 25, \\ 3x -4x > 1 - 7,7 \end{cases}\)
\(\begin{cases} -7x \leq -21, / : (-7) \\ -x > -6,7 / : (-1) \end{cases}\)
\(\begin{cases} x \geq 3, \\ x < 6,7 \end{cases}\)
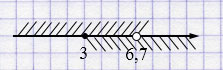
Ответ: \([3; 6,7)\).
Пояснения:
Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.
При решении неравенств системы используем то, что:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Если знак неравенства строгий (\(>\) или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.
Если знак неравенства нестрогий (\(\geq\) или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.
У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.
Вернуться к содержанию учебника