Упражнение 872 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 194
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№872 учебника 2023-2025 (стр. 194):
Зная, что \(5 < x < 8\), оцените значение выражения:
а) \(6x\);
б) \(-10x\);
в) \(x - 5\);
г) \(3x + 2\).
№872 учебника 2013-2022 (стр. 194):
Решите графически уравнение \(\frac{12}{x} = x^2\).
Подсказка
№872 учебника 2023-2025 (стр. 194):
Вспомните свойства числовых неравенств.
№872 учебника 2013-2022 (стр. 194):
Вспомните:
- График обратной пропорциональности (гипербола).
- Положение точек на координатной плоскости.
- Деление и дроби.
- Деление рациональных чисел.
- График квадратичной функции (парабола).
- Степень с натуральным показателем.
Ответ
№872 учебника 2023-2025 (стр. 194):
а) \(5 < x < 8 \)
\(6\cdot5 < 6x < 6\cdot8 \)
\(30 < 6x < 48\).
б) \(5 < x < 8 \)
\(5 < x < 8 \)
\(-10\cdot8 < -10x < -10\cdot5\)
в) \(5 < x < 8\)
\(5 - 5 < x - 5 < 8 - 5\)
\(0 < x - 5 < 3\).
г) \(5 < x < 8\)
\(3\cdot5 + 2 < 3x+2 < 3\cdot8 + 2\)
\(17 < 3x + 2 < 26\).
Пояснения:
При оценке значений выражений используем свойства неравенств:
1. Если к частям неравенства прибавить или вычесть одно и то же число, знак неравенства сохраняется.
2. Если части неравенства умножить или разделить на одно и то же положительное число, знак неравенства сохраняется.
3. Если части неравенства умножить или разделить на одно и то же отрицательное число, знак неравенства меняется на противоположный.
№872 учебника 2013-2022 (стр. 194):
\(\frac{12}{x} = x^2\).
\(y= \frac{12}{x}\)
| \(x\) | 12 | 6 | 4 | 3 | 2 | 1 |
| \(y\) | 1 | 2 | 3 | 4 | 6 | 12 |
| \(x\) | -12 | -6 | -4 | -3 | -2 | -1 |
| \(y\) | -1 | -2 | -3 | -4 | -6 | -12 |
\(y = x^2\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
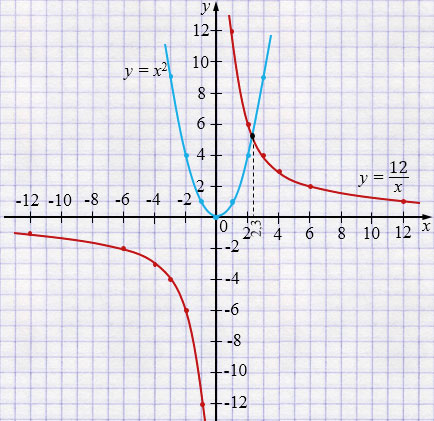
Ответ: \(x \approx 2,3\).
Пояснения:
Чтобы решить графически уравнение \(\displaystyle \frac{12}{x} = x^2\), нужно найти точки пересечения двух графиков:
\(y=\frac{12}{x}\) и \(y = x^2\), где
\(y= \frac{12}{x}\) - функция обратной пропорциональности, графиком является гипербола (две ветви, расположенные в I и III координатных четвертях, так как \(k=12 >0\)). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
\(y = x^2\) - квадратичная функция, графиком которой является парабола. Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
Решением уравнения являются значения координаты \(x\) для точек пересечения графиков.
Вернуться к содержанию учебника