Упражнение 777 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\[x^2 - 15x + q = 0\]

Пусть корни уравнения равны \(x_1\) и  \(x_2\).

По теореме Виета:

\[ x_1 + x_2 = 15, \quad x_1 x_2 = q. \]

\( x_1^2 + x_2^2 = 153\)

\(x_1^2 + 2x_1x_2+ x_2^2 - 2x_1x_2= 153\)

\((x_1 + x_2)^2 - 2x_1x_2=153\)

\(15^2 - 2q =153\)

\(225 - 2q = 153 \)

\( 2q = 225 - 153\)

\(2q= 72\)

\(q = \frac{72}{2}\)

\( q = 36\)

Ответ: \(q = 36.\)

Пояснения:

Использованные приемы и формулы:

- квадрат суммы двух выражений:

\((x_1 + x_2) = x_1^2 + 2x_1x_2 + x_2^2\).

- значение выражения не изменится, если к нему прибавить и вычесть одно и то же выражение, поэтому:

\( x_1^2 + x_2^2 =\)

\(=x_1^2 + 2x_1x_2+ x_2^2 - 2x_1x_2=\)

\(=(x_1 + x_2)^2 - 2x_1x_2\)

- теорема Виета:

\[ x_1 + x_2 = -p, \quad x_1 x_2 = q. \]

Подставив по теореме Виета

\(x_1+x_2=15\), \(x_1x_2=q\), получили уравнение \(225 - 2q = 153\), из которого нашли \(q = 36\).

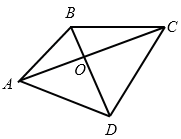
\(ABCD\) - выпуклый четырехугольник.

\(AC\) и \(BD\) - диагонали.

Доказать:

\[AB + CD < AC + BD.\]

Доказательство:

1) В \(\Delta AOB\) по неравенству треугольника:

\(AB < AO + OB\)

2) В \(\Delta COD\) по неравенству треугольника:

\(CD < DO + OC\)

3) \(AB + CD < (AO + OB) + (DO +OC)\)

\(AB + CD < (AO + OC) + (DO +OB)\)

\(AB + CD < AC + BD\)

Что и требовалось доказать.

Пояснения:

Основное свойство, которое используется в доказательстве, — неравенство треугольника: сумма длин двух сторон треугольника больше длины третьей стороны.

Мы рассмотрели треугольники АОВ и COD и сложили соответствующие неравенства, учитывая то, что если почленно сложить верные неравенства одного знака, то получится верное неравенство. Получили неравенство, которое говорит о том, что для выпуклого четырёхугольника сумма длин противоположных сторон действительно меньше суммы длин его диагоналей. Что и требовалось доказать.