Упражнение 175 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

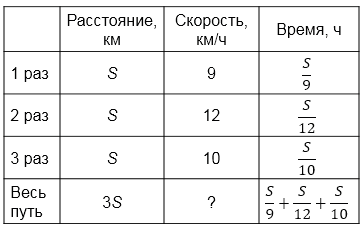
\(v_{ср.} = \frac{3S}{\frac{S}{9} ^{\color{blue}{\backslash20}} +\frac{S}{12} ^{\color{blue}{\backslash15}}+\frac{S}{10} ^{\color{blue}{\backslash18}} }=\)

\(=\frac{3S}{\frac{20S+15S+18S}{180}}=\frac{3S}{\frac{53S}{180}}=\)

\(=3S : \frac{53S}{180}=2S \cdot \frac{180}{53S}=\)

\(=\frac{360\cancel{S}}{53\cancel{S}}=\frac{360}{53}=6\frac{42}{53}\) (км/ч)

Ответ: средняя скорость школьника на всем пути следования равна \(6\frac{42}{53}\) км/ч.

Пояснения:

Использованные правила и приёмы:

• Формула средней скорости при равном расстоянии: общее расстояние, делённое на общее время.

• Время пути рассчитывается как отношение расстояния к скорости: \(\;t = \frac{S}{v}.\)

Пояснения к шагам:

— Сначала ввели переменную \(S\) для расстояния, чтобы не зависеть от конкретного значения.

— Посчитали время движения в каждую сторону по формуле \(t = \frac{S}{v}\).

— Сложили полученные времена и сложили расстояния.

— Разделили общее расстояние на общее время, получили среднюю скорость.

а) \(y=3x\)

\( y = kx + b \)

\(k=3\) и точка \((0;4)\):

\( 4 = 3\cdot0 + b \)

\(b = 4. \)

Уравнение прямой:

\( y = 3x + 4. \)

б) \(y=-\frac12x-8\) 

\( y = kx + b \)

\(k=-\frac12\) и точка \((0;0)\):

\( y = -\tfrac12x + b \)

\( 0 = -\tfrac12\cdot0 + b \)

\(b = 0. \)

Уравнение прямой:

\( y = -\frac12x. \)

Пояснения:

• Две прямые параллельны, если у них одинаковый угловой коэффициент \(k\).

• Общее уравнение прямой с угловым коэффициентом \(k\):

\(\;y = kx + b,\) где \(b\) - числовой коэффициент.

• Для нахождения \(b\) подставляем координаты данной точки в уравнение и решаем относительно \(b\).

— В пункте а) через \((0;4)\) и \(k=3\) получили \(b=4\).

— В пункте б) через \((0;0)\) и \(k=-\frac12\) получили \(b=0\).