Упражнение 1086 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\( f(x) = -2\sqrt{x} \)

\(f(0) = -2\sqrt{0} = 0\)

\(f(0,25) = -2\sqrt{0,25} = -1\)

\(f(1) = -2\sqrt{1} = -2\)

\(f(2,25) = -2\sqrt{2,25} = -3\)

\(f(4) = -2\sqrt{4} = -4\)

\(f(6,25) = -2\sqrt{6,25} = -5\)

\(f(9) = -2\sqrt{9} = -6\)

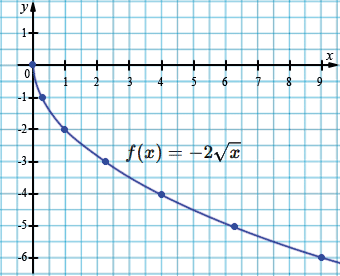
1. Значения данной функции с увеличением значений аргумента от \(0\) до \(+\infty\) уменьшается.

2. \(D(f) = [0; +\infty)\).

3.  \(E(f) = (-\infty; 0]\).

Пояснения:

Функция содержит квадратный корень, поэтому область определения ограничена условием \(x \geq 0\).

Так как функция имеет вид \(f(x) = -2\sqrt{x}\), при возрастании аргумента \(x\) увеличивается \(\sqrt{x}\), но множитель «-2» делает результат отрицательным и всё меньше при увеличении \(x\).

Следовательно, функция убывает на всём множестве своих значений.

Наибольшее значение функции равно \(0\) при \(x=0\). Наименьшего значения нет, так как при \(x \to +\infty\) функция стремится к \(-\infty\).

Таким образом:

Область определения: \([0; +\infty)\).

Множество значений: \((-\infty; 0]\).

а) \( x^{-2} + x^{-1} + x = \)

\(=x \left(x^{-3} + x^{-2} + 1\right). \)

б) \( x^{-2} + x^{-1} + x = \)

\(=x^{-1}\left(x^{-1} + 1 + x^{2}\right). \)

в) \( x^{-2} + x^{-1} + x =\)

\(=x^{-2}\left(1 + x + x^{3}\right). \)

Пояснения:

Учитываем свойство степени:

\(a^ma^n = a^{m+n}\).

Подробное решение:

а) \( x^{-2} + x^{-1} + x = \)

\(= x^{-3+1} + x^{-2+1} + x = \)

\(= x^{-3}x + x^{-2}x + x = \)

\(=x \left(x^{-3} + x^{-2} + 1\right). \)

б) \( x^{-2} + x^{-1} + x = \)

\( =x^{-1-1} + x^{-1} + x^{-1+2} = \)

\( =x^{-1}x^{-1} + x^{-1} + x^{-1}x^2 = \)

\(=x^{-1}\left(x^{-1} + 1 + x^{2}\right). \)

в) \( x^{-2} + x^{-1} + x =\)

\( =x^{-2} + x^{-2 +1} + x^{-2 + 3} =\)

\( =x^{-2} + x^{-2}x^{1} + x^{-2}x^{3} =\)

\(=x^{-2}\left(1 + x + x^{3}\right). \)