Упражнение 975 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№975 учебника 2023-2025 (стр. 219):
Решите систему неравенств:
а) \(\begin{cases} x > 17, \\ x > 12; \end{cases}\)
б) \(\begin{cases} x < 1, \\ x < 5; \end{cases}\)
в) \(\begin{cases} x > 0, \\ x < 6; \end{cases}\)
г) \(\begin{cases} x < -3,5, \\ x > 8; \end{cases}\)
д) \(\begin{cases} x \geq -1, \\ x \leq 3; \end{cases}\)
е) \(\begin{cases} x > 8, \\ x \leq 20; \end{cases}\)
№975 учебника 2013-2022 (стр. 216):
Найдите значения выражений \(x^n\) и \(x^{-n}\), если:
а) \(x = \dfrac{2}{3}, \; n = -2;\)
б) \(x = -1{,}5, \; n = 3.\)
Подсказка
№975 учебника 2023-2025 (стр. 219):
Вспомните:
- Что называют решением системы неравенств с одной переменной.
- Числовые промежутки.
№975 учебника 2013-2022 (стр. 216):
Вспомните:
- Степень с целым отрицательным показателем.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Обыкновенные дроби.
- Смешанные числа.
- Десятичная запись дробных чисел.
- Взаимно обратные дроби.
Ответ
№975 учебника 2023-2025 (стр. 219):
а) \(\begin{cases} x > 17, \\ x > 12 \end{cases}\)
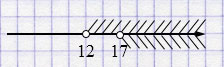
Ответ: \((17; +\infty)\).
б) \(\begin{cases} x < 1, \\ x < 5 \end{cases}\)
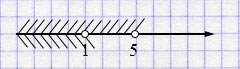
Ответ: \((-\infty; 1)\).
в) \(\begin{cases} x > 0, \\ x < 6 \end{cases}\)
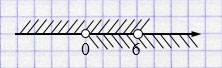
Ответ: \((0; 6)\)
г) \(\begin{cases} x < -3,5, \\ x > 8 \end{cases}\)
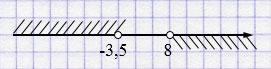
Ответ: решений нет.
д) \(\begin{cases} x \geq -1, \\ x \leq 3 \end{cases}\)

е) \(\begin{cases} x > 8, \\ x \leq 20 \end{cases}\)
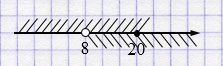
Ответ: \((8; 20]\).
Пояснения:
Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.
Если знак неравенства строгий (\(>\) или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.
Если знак неравенства нестрогий (\(\geq\) или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.
У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.
№975 учебника 2013-2022 (стр. 216):
а) Если \(x = \dfrac{2}{3}, \; n = -2\), то
\(x^n = \left(\dfrac{2}{3}\right)^{-2} = \left(\dfrac{3}{2}\right)^2 = \dfrac{9}{4}\)
\(x^{-n} = \left(\dfrac{2}{3}\right)^{2} = \dfrac{4}{9}\)
б) Если \(x = -1{,}5, \; n = 3\), то
\(x^n = (-1{,}5)^3 = (-\dfrac{3}{2})^3 =\)
\(=-\dfrac{27}{8}= -3\dfrac{3}{8}\)
\(x^{-n} = (-1{,}5)^{-3} = (-\dfrac{3}{2})^{-3} = \)
\(=(-\dfrac{2}{3})^{3} = -\dfrac{8}{27} \)
Пояснения:
Основные правила:
\( a^{-n} = \frac{1}{a^n},\)
\(\left(\frac{a}{b}\right)^{-n} = \left(\frac{b}{a}\right)^n = \frac{b^n}{a^n}\).
1. Показатель со знаком «−» означает, что нужно взять обратное число к степени с положительным показателем.
2. Если основание отрицательное, знак результата зависит от чётности степени: при нечётной — минус, при чётной — плюс.
3. Для дробных оснований с отрицательными степенями выполняется обращение дроби: \(\left(\dfrac{a}{b}\right)^{-n} = \left(\dfrac{b}{a}\right)^n.\)
Таким образом, каждая пара значений \(x^n\) и \(x^{-n}\) связана обратной зависимостью: одно — дробное, другое — его обратное число.
Вернуться к содержанию учебника