Упражнение 321 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№321 учебника 2023-2025 (стр. 77):
Найдите квадрат числа:
\(\sqrt{25};\;\sqrt{81};\;\sqrt{2};\;\sqrt{3};\;-\sqrt{4};\)
\(\sqrt{5};\;-\sqrt{6};\;\sqrt{\tfrac{1}{2}};\;\sqrt{1{,}3}.\)
№321 учебника 2013-2022 (стр. 79):
Решите уравнение и с помощью графика функции \(y = x^2\) найдите приближённые значения его корней:
а) \(x^2 = 3\);
б) \(x^2 = 5\);
в) \(x^2 = 4{,}5\);
г) \(x^2 = 8{,}5\).
Подсказка
№321 учебника 2023-2025 (стр. 77):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
№321 учебника 2013-2022 (стр. 79):
Вспомните:
- Квадратичная функция, ее график.
- Корни уравнения вида \(x^2 = a\).
Ответ
№321 учебника 2023-2025 (стр. 77):
а) \(\bigl(\sqrt{25}\bigr)^2 = 25\).
б) \(\bigl(\sqrt{81}\bigr)^2 = 81\).
в) \(\bigl(\sqrt{2}\bigr)^2 = 2\).
г) \(\bigl(\sqrt{3}\bigr)^2 = 3\).
д) \(\bigl(-\sqrt{4}\bigr)^2 = 4\).
е) \(\bigl(\sqrt{5}\bigr)^2 = 5\).
ж) \(\bigl(-\sqrt{6}\bigr)^2 = 6\).
з) \(\bigl(\sqrt{\frac{1}{2}}\bigr)^2 = \frac{1}{2}\).
и) \(\bigl(\sqrt{1{,}3}\bigr)^2 = 1{,}3\).
Пояснения:
Использованные правила:
1) Квадрат квадратного корня:
\(\bigl(\sqrt{A}\bigr)^2 = A\) при \(A\ge0\).
2) Квадрат минус корня:
\(\bigl(-\sqrt{A}\bigr)^2 = (-1)^2\cdot\bigl(\sqrt{A}\bigr)^2 = A\).
Для всех случаев подкоренное выражение неотрицательно, поэтому можно применять правила.
№321 учебника 2013-2022 (стр. 79):
а) \(y = x^2\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
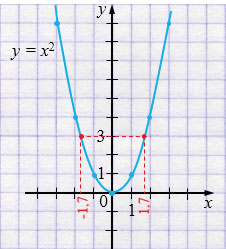
\(x^2 = 3\)
\(x_1 =-1,7\) и \(x_2 = 1{,}7\)
Ответ: \(x_1 =-1,7\) и \(x_2 = 1{,}7\).
б) \(y = x^2\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
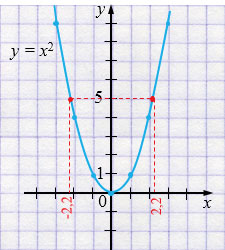
\(x^2 = 5\)
\(x_1 = -2,2\) и \(x_2 = 2,2\)
Ответ: \(x_1 = -2,2\) и \(x_2 = 2,2\).
в) \(y = x^2\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
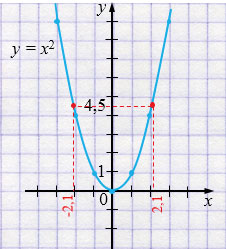
\(x^2 = 4,5\)
\(x_1 =-2,1\) и \(x_2 = 2,1\)
Ответ: \(x_1 =-2,1\) и \(x_2 = 2,1\).
г) \(y = x^2\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
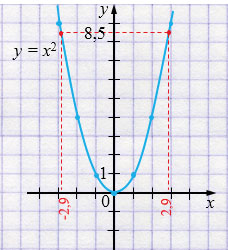
\(x^2 = 8,5\)
\(x_1 =- 2{,}9\) и \(x_2 = 2{,}9\)
Ответ: \(x_1 =- 2{,}9\) и \(x_2 = 2{,}9\).
Пояснения:
\(y = x^2\) - квадратичная функция, графиком является парабола. Строим график по точкам приведенным в таблице.
а) Чтобы решить уравнение \(x^2 = 3\) с помощью графика функции \(y = x^2\), нужно провести прямую, параллельную оси \(x\), через значение на оси \(y\), равное 3, эта прямая пересечет параболу в двух точках, из этих точек нужно провести прямые, перпендикулярные оси \(x\). Точки пересечения перпендикулярных прямых с осью \(x\), укажут два решения уравнения \(x^2 = 3\):
\(x_1 =-1,7\) и \(x_2 = 1{,}7\).
В пунктах б), в) и г) рассуждаем аналогично.
Вернуться к содержанию учебника