Упражнение 1145 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 227
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1145 учебника 2023-2025 (стр. 227):
Покажите штриховкой множество точек координатной плоскости, которое задаёт неравенство:
а) \(y \ge x\);
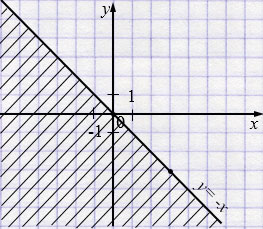
б) \(y \le -x\);
в) \(x \ge 1\);
г) \(y \le 5\).
№1145 учебника 2013-2022 (стр. 227):
К двузначному числу приписали слева и справа по 1. Получившееся четырёхзначное число оказалось в 21 раз больше первоначального. Найдите двузначное число.
Подсказка
№1145 учебника 2023-2025 (стр. 227):
Вспомните:
№1145 учебника 2013-2022 (стр. 227):
Вспомните:
- Запись многозначного числа в виде многочлена.
- Линейное уравнение с двумя переменными, его свойства.
- Раскрытие скобок, подобные слагаемые.
- Целые числа.
Ответ
№1145 учебника 2023-2025 (стр. 227):
а) \(y \ge x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |

б) \(y \le -x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | -3 |
в) \(x \ge 1\)

г) \(y \le 5\)

Пояснения:
1) Для неравенства вида \(y \ge kx + b\) или \(y \le kx + b\) проводят границу линию и закрашивают полуплоскость, где неравенство истинно. Если знак «\(\ge\)» или «\(\le\)», граница включается (штриховка до линии).
2) Для неравенств \(x \ge c\) или \(x \le c\) проводят вертикальную линию \(x=c\) и штрихуют соответствующую полуплоскость (справа или слева от прямой).
3) Аналогично для \(y \ge c\) или \(y \le c\) проводят горизонтальную линию \(y=c\) и штрихуют область выше или ниже неё.
а) \(y \ge x\): прямая \(y=x\) — граница. Штриховка области над и на этой прямой. Точки на прямой включаются.
б) \(y \le -x\): прямая \(y=-x\) — граница. Штриховка области под и на этой прямой (слева-внизу). Точки на прямой включаются.
в) \(x \ge 1\): вертикальная прямая \(x=1\). Штриховка области справа от неё (включая саму линию).
г) \(y \le 5\): горизонтальная прямая \(y=5\). Штриховка области ниже неё (включая саму линию).
№1145 учебника 2013-2022 (стр. 227):
Пусть \(x\) - десятки исходного двузначного числа, а \(y\) - единицы. Тогда исходное число \(\overline{xy}\), а новое число \(\overline{1xy1}\). Известно, что новое число в 21 раз больше исходного.
Составим уравнение:
\(\overline{1xy1} = 21\overline{xy}\)
\(1000 + 100x + 10y + 1 = 21(10x + y) \)
\(1001 + 100x + 10y = 210x + 21y \)
\( 1001 + 100x + 10y - 210x - 21y = 0 \)
\(1001 - 110x - 11y = 0\) / \( :11\)
\( 91 - 10x - y = 0 \)
\(10x + y = 91 \)
\(\overline{xy}=91\)
\(x=9,\; y=1\).
\(\overline{xy} = 91\)
Ответ: 91.
Пояснения:
– Представление трёхзначного числа через цифры: если оно \(\overline{ab}\), то равно \(10a + b\).
– Приписывание цифры «1» слева и справа преобразует число в
\(1000\cdot1 + 100x + 10y + 1\).
– По условию составлено уравнение, затем раскрыты скобки и приведены подобные члены.
– Деление уравнения на общий множитель 11 упростило его до
\(10x + y = 91\).
– Учтено ограничение: \(x\) и \(y\) — цифры, поэтому единственный вариант:
\(x=9\), \(y=1\).
– Окончательный ответ: \(91\).
Вернуться к содержанию учебника