Задание 4.358 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 66
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№4.358 учебника 2021-2022 (стр. 66):
Можно ли дробь 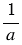 , если
, если
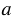 = 4;
= 4; 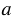 = 25;
= 25; 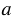 = 6;
= 6; 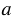 = 8:
= 8:
а) представить в виде десятичной дроби;
б) привести к знаменателю 100?
Подсказка
№4.358 учебника 2021-2022 (стр. 66):
Вспомните:
- Обыкновенные дроби.
- Несократимая дробь.
- Какие числа называют простыми.
- Разложение на простые множители.
- Десятичная запись дробных чисел.
- Приведение дробей к новому знаменателю.
Ответ
№4.358 учебника 2021-2022 (стр. 66):
а) Если 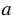 = 4 = 2 • 2, то дробь
= 4 = 2 • 2, то дробь 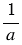 можно представить в виде конечной десятичной дроби.
можно представить в виде конечной десятичной дроби.
Если 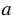 = 25 = 5 • 5, то дробь
= 25 = 5 • 5, то дробь 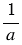 можно представить в виде конечной десятичной дроби.
можно представить в виде конечной десятичной дроби.
Если 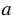 = 6 = 2 • 3, то дробь
= 6 = 2 • 3, то дробь 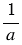 нельзя представить в виде конечной десятичной дроби.
нельзя представить в виде конечной десятичной дроби.
Если 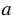 = 8 = 2 • 2 • 2, то дробь
= 8 = 2 • 2 • 2, то дробь 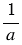 можно представить в виде конечной десятичной дроби.
можно представить в виде конечной десятичной дроби.
б) Если 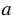 = 4 и
= 4 и 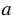 = 25, то дробь
= 25, то дробь 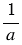 можно привести к знаменателю 100, так как 100 : 4 = 25 и 100 : 25 = 4.
можно привести к знаменателю 100, так как 100 : 4 = 25 и 100 : 25 = 4.
Если 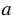 = 6 и
= 6 и 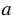 = 8, то дробь
= 8, то дробь 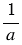 нельзя привести к знаменателю 100, так как 100 не делится нацело на 6 и 8.
нельзя привести к знаменателю 100, так как 100 не делится нацело на 6 и 8.
Пояснения:
а) Если в разложении знаменателя несократимой дроби на простые множители содержатся простые числа, отличные от 2 и 5, то эту дробь нельзя представить в виде конечной десятичной дроби. Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получится несократимая дробь.
Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число. Натуральное число называют составным, если оно имеет больше двух натуральных делителей.
Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.
б) Дробь можно привести к новому знаменателю только в том случае, если новый знаменатель делится нацело на старый знаменатель дроби.
Вернуться к содержанию учебника