Задание 2.253 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.253 учебника 2023-2024 (стр. 77):
Береза выше ели на  м, а сосна выше березы
м, а сосна выше березы  м. Какой высоты ель и сосна, если высота березы составляет
м. Какой высоты ель и сосна, если высота березы составляет 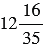 м?
м?
№2.253 учебника 2021-2022 (стр. 71):
Выполните действия:

Подсказка
№2.253 учебника 2023-2024 (стр. 77):
Вспомните:
- Оформление задач.
- Сложение и вычитание смешанных чисел.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Наименьшее общее кратное.
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Основное свойство дроби.
- Неправильные дроби.
- Десятичные дроби.
№2.253 учебника 2021-2022 (стр. 71):
Вспомните:
- Сложение и вычитание смешанных чисел.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Наименьшее общее кратное.
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Основное свойство дроби.
- Неправильные дроби.
- Свойства вычитания.
- Свойства сложения.
Ответ
№2.253 учебника 2023-2024 (стр. 77):
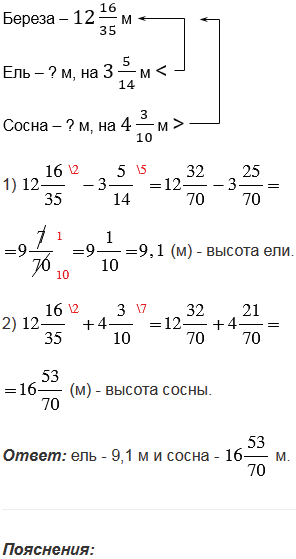


№2.253 учебника 2021-2022 (стр. 71):
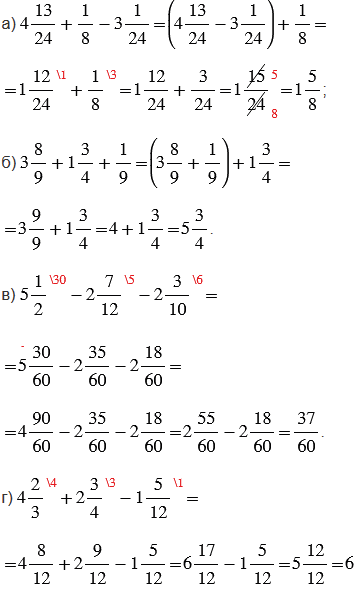
Пояснения:
При выполнении вычислений в пункте а) для упрощения вычислений применяем свойство вычитания числа из сумы.
При выполнении вычислений в пункте б) для упрощения вычислений применяем переместительное и сочетательное свойства сложения.
Вычисления в пунктах в) и г) выполняем по порядку слева направо.
Чтобы найти сумму смешанных чисел, надо:
1) дробные части этих чисел привести к наименьшему общему знаменателю;
2) отдельно выполнить сложение целых и отдельно дробных частей;
3) при необходимости сократить дробь (разделить числитель и знаменатель дроби на их наибольший общий делитель), выделить целую часть (когда числитель больше знаменателя) и прибавить ее к полученной целой части.
Чтобы найти разность смешанных чисел, надо:
1) дробные части этих чисел привести к наименьшему общему знаменателю;
2) если дробная часть уменьшаемого больше дробной части вычитаемого, то надо отдельно вычесть целые и отдельно дробные части и результаты сложить;
3) если дробная часть уменьшаемого меньше дробной части вычитаемого, то надо превратить ее в неправильную дробь, уменьшив на единицу целую часть, и выполнить вычитание по пункту 2;
4) при необходимости сократить дробь (разделить числитель и знаменатель дроби на их наибольший общий делитель).
Также помним, дробь, у которой числитель и знаменатель одинаковые, равна единице.
Вернуться к содержанию учебника