Задание 2.84 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.84 учебника 2023-2024 (стр. 53):
Развивай мышление. Представьте в виде суммы с наименьшим числом простых слагаемых (слагаемые могут повторяться) числа:
а) нечётные, большие 5, но меньшие 20;
б) чётные, большие 2, но меньшие 20.
Сформулируйте предложения о представлении чисел в виде суммы простых слагаемых.
№2.84 учебника 2021-2022 (стр. 47):
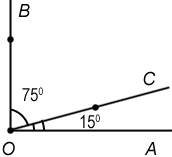
1) Прямой угол АОВ разделён на два угла: АОС и СОВ. Чему равны эти углы, если угол СОВ в 5 раз больше угла АОС? Постройте эти углы.
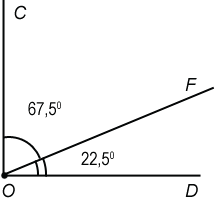
2) Прямой угол COD разделен на два угла: COF и FOD. Чему равны эти углы, если угол FOD в 3 раза меньше угла COF? Постройте эти углы.
Подсказка
№2.84 учебника 2023-2024 (стр. 53):
Вспомните:
- Какие числа называют простыми.
- Какие числа называют четными, нечетными.
- Сложение и вычитание натуральных чисел.
№2.84 учебника 2021-2022 (стр. 47):
Вспомните:
- Как использовать транспортир.
- Что такое угол.
- Измерение углов.
- Что такое уравнение.
- Что называют корнем уравнения.
Ответ
№2.84 учебника 2023-2024 (стр. 53):
а) 7 = 5 + 2; 9 = 7 + 2; 11 = 7 + 2 + 2;
13 = 11 + 2; 15 = 13 +2; 17 = 11 + 3 + 3,
19 = 17 + 2.
б) 4 = 2 + 2; 6 = 3 + 3; 8 = 5 + 3;
10 = 5 + 5; 12 = 7 + 5;
14 = 11 + 3; 16 = 13 + 3; 18 = 13 + 5.
Любое число можно представить в виде суммы простых чисел, причем не единственным способом.
Пояснения:
Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число.
Обратите внимание, что 1 не относят ни к составным числам, ни к простым, так как оно имеет только один делитель.
Числа, делящиеся без остатка на 2, называют чётными, а числа, которые при делении на 2 дают остаток 1, называют нечётными.
№2.84 учебника 2021-2022 (стр. 47):
1) 
АОС + СОВ = 900;
СОВ = 5АОС;
АОС + 5АОС = 900;
6АОС = 900;
АОС = 900:6;
| - | 9 | 0 | 6 | ||||
| 6 | 1 | 5 | |||||
| - | 3 | 0 | |||||
| 3 | 0 | ||||||
| 0 |
АОС =150;
СОВ = 5АОС = 5•150 = 750.
2) COF + FOD = 900;
COF = 3FOD;
3FOD + FOD = 900;
4FOD = 900;
FOD = 900:4;
| - | 9 | 0 | 4 | |||||
| 8 | 2 | 2 | , | 5 | ||||
| - | 1 | 0 | ||||||
| 8 | ||||||||
| - | 2 | 0 | ||||||
| 2 | 0 | |||||||
| 0 |
FOD = 22,50;
COF = 3FOD = 3•22,50 = 67,50.
| × | 2 | 2 | 5 |
| 3 | |||
| 6 | 7 | 5 |
Пояснения:
Для того чтобы начертить угол с заданной градусной мерой, необходимо совместить начало луча, который определяет одну из сторон угла, с центром транспортира, так, чтобы этот луч прошел через нулевое деление шкалы транспортира, найти на шкале транспортира нужную градусную меру и провести через это значение вторую сторону угла.
Чтобы построить углы АОС = 150 и АОВ = 900, чертим луч ОА и прикладываем центр транспортира к точке О, так, чтобы луч ОА прошел через нулевое деление на внутренней шкале транспортира, и находим на внутренней шкале транспортира значения 150 и 900, ставим напротив них точки.
Чертим лучи с началом в точке О, которые пройдут через отмеченные точки, получаем
АОС = 150 и АОВ = 900.
Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
В рассматриваемом случае
АОВ = СОВ + АОС, откуда
СОВ = АОВ - АОС, значит,
СОВ = 900 - 150 = 750.
Вернуться к содержанию учебника