Задание 2.79 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.79 учебника 2023-2024 (стр. 53):
Используя транспортир, постройте 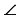 KLM=650 и
KLM=650 и 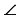 PRS=1700.
PRS=1700.
№2.79 учебника 2021-2022 (стр. 47):
Существует ли четыре таких различных простых числа, что произведение двух из них равно произведению двух других?
Подсказка
№2.79 учебника 2023-2024 (стр. 53):
Вспомните:
- Как использовать транспортир.
- Что такое угол.
- Измерение углов.
№2.79 учебника 2021-2022 (стр. 47):
Вспомните:
- Какие числа называют простыми и составными.
- Разложение на простые множители.
Ответ
№2.79 учебника 2023-2024 (стр. 53):

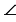 KLM=650.
KLM=650.

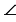 PRS=1700.
PRS=1700.
Пояснения:
Для того чтобы начертить угол с заданной градусной мерой, необходимо совместить начало луча, который определяет одну из сторон угла, с центром транспортира, так, чтобы этот луч прошел через нулевое деление шкалы транспортира, найти на шкале транспортира нужную градусную меру и провести через это значение вторую сторону угла.
Чтобы построить угол KLM=650, чертим луч LM и прикладываем центр транспортира к точке L, так, чтобы луч LM прошел через нулевое деление на внутренней шкале транспортира, и находим на внутренней шкале транспортира значение 650, ставим напротив него точку.

Чертим луч с началом в точке L, который пройдет через отмеченную точку, получаем 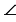 KLM=650.
KLM=650.

Второй угол строим аналогично.
№2.79 учебника 2021-2022 (стр. 47):
Таких чисел не существует.
Пояснения:
Произведение двух простых чисел - это составное число. Пусть a, b, c, d - различные простые числа. Запишем произвольные произведения пар этих чисел, например:
a•b, c•d.
Так как числа простые, то данные произведения являются разложениями чисел на простые множители, а так как любое составное число можно представить в виде простых множителей единственным способом, то a•b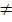 c•d, а следовательно, не существует четырех таких различных простых числа, что произведение двух из них равно произведению двух других.
c•d, а следовательно, не существует четырех таких различных простых числа, что произведение двух из них равно произведению двух других.
Вернуться к содержанию учебника