Задание 3.29 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 123
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№3.29 учебника 2023-2024 (стр. 123):
№3.29 учебника 2021-2022 (стр. 123):
Вычислите объем прямоугольного параллелепипеда, у которого:
1) ширина 1,5 м и составляет 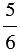 длины, а высота в 1,8 раза меньше длины;
длины, а высота в 1,8 раза меньше длины;
2) длина 15,3 м и составляет 0,9 высоты, а высота в 3,4 раза больше ширины.
Подсказка
№3.29 учебника 2023-2024 (стр. 123):
№3.29 учебника 2021-2022 (стр. 123):
Вспомните:
- Что называют прямоугольным параллелепипедом, как найти его объем.
- Деление обыкновенных дробей, как найти целое по его части.
- Умножение обыкновенных дробей, взаимно обратные числа.
- Десятичная запись дробных чисел.
- Сокращение дробей.
- Деление десятичных дробей.
- Умножение десятичных дробей.
Ответ
№3.29 учебника 2023-2024 (стр. 123):
№3.29 учебника 2021-2022 (стр. 123):

2) 1,8 : 1,8 = 1 (м) - высота прямоугольного параллелепипеда.
3) 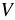 = 1,5 • 1,8 • 1 = 2,7 (м3)
= 1,5 • 1,8 • 1 = 2,7 (м3)
| × | 1 | 5 | |
| 1 | 8 | ||
| + | 1 | 2 | 0 |
| 1 | 5 | ||
| 2 | 7 | 0 |
Ответ: объем прямоугольного параллелепипеда равен 2,7 м3.
2) 1) 15,3 : 0,9 = 153 : 9 = 17 (м) - высота прямоугольного параллелепипеда.
| - | 1 | 5 | 3 | 9 | ||||||||||
| 9 | 1 | 7 | ||||||||||||
| - | 6 | 3 | ||||||||||||
| 6 | 3 | |||||||||||||
| 0 |
2) 17 : 3,4 = 170 : 34 = 5 (м) - ширина прямоугольного параллелепипеда
3) 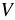 = 15,3 • 17 • 5 = 260,1 • 5 = 1300,5 (м3)
= 15,3 • 17 • 5 = 260,1 • 5 = 1300,5 (м3)
|
|
Ответ: объем прямоугольного параллелепипеда равен 1300,5 м3.
Пояснения:
Объем прямоугольного параллелепипеда равен произведению трех его измерений (длины, ширины и высоты).
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
1) Ширина 1,5 м и составляет 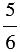 длины, значит, длина прямоугольного параллелепипеда равна:
длины, значит, длина прямоугольного параллелепипеда равна:

Чтобы выполнить деление, десятичную дробь преобразовали в обыкновенную дробь. Чтобы найти частное двух дробей, надо делимое умножить на число, обратное делителю. При этом помним, обратным числу 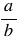 является число
является число 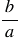 . При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
. При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Длина прямоугольного параллелепипеда 1,8 м, а высота в 1,8 раза меньше длины, значит, высота прямоугольного параллелепипеда равна:
1,8 : 1,8 = 1 (м).
Итак, длина прямоугольного параллелепипеда равна 1,8 м, ширина - 1,5 м, а высота - 1 м, значит, его объем:
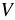 = 1,5 • 1,8 • 1 = 2,7 (м3).
= 1,5 • 1,8 • 1 = 2,7 (м3).
2) Алгоритм, по которому находим объем прямоугольного параллелепипеда, у которого длина 15,3 м и составляет 0,9 высоты, а высота в 3,4 раза больше ширины, такой же как и в первом пункте.
Вернуться к содержанию учебника