Задание 2.43 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Выберите год учебника
Вопрос
№2.43 учебника 2023-2024 (стр. 48):
1) За два перегона поезд проехал 156,5 км. При этом первый перегон был короче второго на 17,8 км. Найдите протяженность каждого перегона.
2) Междугородный автобус сделал в пути одну остановку. При этом расстояние от начала маршрута до остановки оказалось на 23,7 км больше, чем остальной путь. Найдите расстояние до остановки и после нее, если протяженность всего пути составила 142,4 км.
№2.43 учебника 2021-2022 (стр. 42):
Вычислите значение выражения:
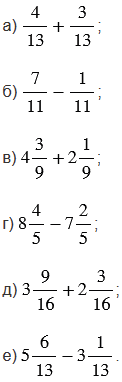
Подсказка
№2.43 учебника 2023-2024 (стр. 48):
Вспомните:
- Оформление задач.
- Что называют уравнением, его корни.
- Сложение и вычитание десятичных дробей.
- Деление десятичных дробей.
№2.43 учебника 2021-2022 (стр. 42):
Вспомните:
- Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями.
- Сложение и вычитание смешанных чисел.
- Сокращение дробей.
Ответ
№2.43 учебника 2023-2024 (стр. 48):
1) Пусть длина первого перегона равна 
км , тогда длина второго перегона равна ( + 17,8) км. Длина двух перегонов 156,5 км.
Составим уравнение:
+ ( + 17,8) = 156,5
( + ) + 17,8 = 156,5
2 + 17,8 = 156,5
2 = 156,5 - 17,8
2 = 138,7
= 138,7 : 2
= 69,35 (км) - первый перегон.
|
|
+ 17,8 = 69,35 + 17,8 = 87,15 (км) - второй перегон.
| + | 6 | 9 | , | 3 | 5 |
| 1 | 7 | , | 8 | 0 | |
| 8 | 7 | , | 1 | 5 |
Ответ: 69,35 км и 87,15 км.
2) Пусть км расстояние после остановки, тогда расстояние до остановки ( + 23,7) км. Весь путь 142,4 км.
Составим уравнение:
( + 23,7) + = 142,4
( + ) + 23,7 = 142,4
2 + 23,7 = 142,4
2 = 142,4 - 23,7
2 = 118,7
= 118,7 : 2
= 59,35 (км) - расстояние после остановки.
|
|
+ 23,7 = 59,35 + 23,7 = 83,05 (км) - расстояние до остановки.
| + | 5 | 9 | , | 3 | 5 |
| 2 | 3 | , | 7 | 0 | |
| 8 | 3 | , | 0 | 5 |
Ответ: 83,05 км и 59,35 км.
Пояснения:
Каждую из задач решаем с помощью уравнения.
1) Пусть км длина первого перегона. Первый перегон короче второго перегона на 17,8 км, то есть второй перегон на 17,8 км длиннее первого, тогда длина второго - ( + 17,8) км. Длина двух перегонов 156,5 км. Значит, можем составить следующее уравнение:
+ ( + 17,8) = 156,5.
Используя сочетательное свойство сложения, получим:
( + ) + 17,8 = 156,5.
2 + 17,8 = 156,5.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое тогда:
2 = 156,5 - 17,8,
2 = 138,7.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
= 138,7 : 2,
= 69,35.
Учитывая обозначения введенные выше, длина первого перегона равна 69,32 км, а длина второго перегона:
+ 17,8 = 69,35 + 17,8 = 87,15 (км).
2) Пусть км расстояние после остановки. Расстояние от начала маршрута до остановки оказалось на 23,7 км больше, чем остальной путь, тогда расстояние до остановки составляет ( + 23,7) км. Весь путь 142,4 км. Значит, можем составить следующее уравнение:
( + 23,7) + = 142,4.
Используя сочетательное свойство сложения, получим:
( + ) + 23,7 = 142,4,
2 + 23,7 = 142,4.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое, тогда:
2 = 142,4 - 23,7,
2 = 118,7.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
= 118,7 : 2,
= 59,35
Учитывая обозначения введенные выше, расстояние после остановки 59,35 км, а расстояние до остановки:
+ 23,7 = 59,35 + 23,7 = 83,05 (км).
№2.43 учебника 2021-2022 (стр. 42):
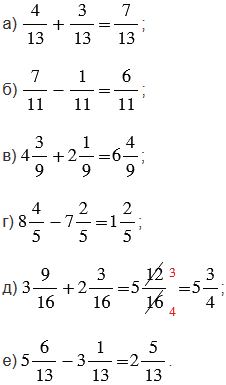
Пояснения:
Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Чтобы найти сумму (разность) двух смешанных чисел, надо отдельно сложить (вычесть) их целые и дробные части.
Если при вычислениях получается сократимая дробь, то сокращаем ее (числитель и знаменатель делим на их общий делитель).
Вернуться к содержанию учебника