Задание 5. Вопросы для повторения к главе VI - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник. Страница 136

Выпуклый четырехугольник - это четырехугольник, каждая диагональ которого разделяет его на два треугольника.

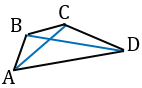
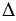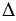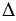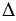В четырехугольнике АВСD диагональ ВD разбивает выпуклый четырехугольник АВСD на АВD и ВСD, а диагональ АС - на АВС и АСD.

Сумма углов выпуклого n-угольника равна (n-2)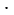180⁰, тогда, учитывая то, что у четырехугольника 4 угла, то есть n = 4, сумма углов выпуклого четырехугольника равна

(4-2)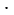180⁰ = 360⁰.