Задание 4. Вопросы для повторения к главе V - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопросы для повторения к главе V. Страница 112, 113
Вопрос
Выберите год учебника
№4 учебника 2013-2022 (стр. 113):
Выведите формулу для вычисления суммы углов выпуклого n-угольника.
№4 учебника 2023-2024 (стр. 112):
Какая прямая называется серединным перпендикуляром к отрезку?
Подсказка
№4 учебника 2013-2022 (стр. 113):
№4 учебника 2023-2024 (стр. 112):
Вспомните:
- Что такое отрезок.
- Что такое перпендикуляр.
- Что такое середина отрезка.
Ответ
№4 учебника 2013-2022 (стр. 113):
Рассмотрим выпуклый n-угольник.
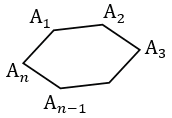
АnА1А2, А1А2А3, ..., Аn-1АnА1 - углы этого многоугольника. Найдем их сумму.
Соединим вершину А1 диагоналями с другими вершинами.
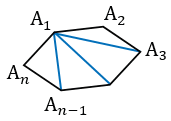
В итоге получим n-2 треугольника, сумма которых равна сумме углов n-угольника. Сумма углов каждого треугольника равна 1800, поэтому сумма углов многоугольника А1А2...Аn равна (n-2) 1800.
1800.
Итак, сумма углов выпуклого n-угольника равна (n - 2) 1800.
1800.
№4 учебника 2023-2024 (стр. 112):

Вернуться к содержанию учебника