Задание 8. Вопросы для повторения к главе V - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник. Страница 113
Старая и новая редакции
Вернуться к содержанию учебника
Вопросы для повторения к главе V. Страница 113
Вопрос
Выберите год учебника
№8 учебника 2013-2022 (стр. 113):
Дайте определение параллелограмма. Является ли параллелограмм выпуклым четырехугольником?
№8 учебника 2023-2024 (стр. 113):
Сформулируйте и докажите свойства диаметра окружности.
Подсказка
№8 учебника 2013-2022 (стр. 113):
Вспомните:
- Какой четырехугольник называется параллелограммом.
- Какой многоугольник называется выпуклым.
№8 учебника 2023-2024 (стр. 113):
Вспомните, что называют окружностью, ее диаметр.
Ответ
№8 учебника 2013-2022 (стр. 113):
Параллелограмм - это выпуклый четырехугольник, у которого противоположные стороны попарно параллельны.
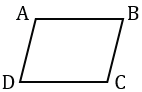
В параллелограмме АВСD, противоположные стороны АВ и DC, АD и ВС параллельны, т.е. АВ 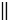 DC, АD
DC, АD 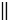 ВС.
ВС.
Пояснения:
Каждая диагональ параллелограмма делит его на два треугольника, поэтому параллелограмм - выпуклый четырехугольник.
№8 учебника 2023-2024 (стр. 113):
Свойства диаметра:
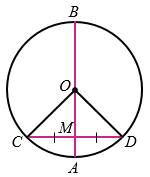
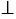 CD.
CD.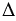 COD равнобедренный (т.к. две его стороны - радиусы окружности), и отрезок ОМ является его медианой. В равнобедренном треугольнике медиана, проведённая к основанию, является также высотой треугольника. Значит, ОМ
COD равнобедренный (т.к. две его стороны - радиусы окружности), и отрезок ОМ является его медианой. В равнобедренном треугольнике медиана, проведённая к основанию, является также высотой треугольника. Значит, ОМ 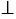 CD, поэтому АВ
CD, поэтому АВ 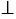 CD.
CD. 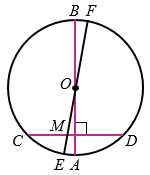
 CD. Но тогда через центр О окружности проходят две прямые AB и EF, перпендикулярные CD, значит, они совпадают. Поэтому EF и AB — один и тот же диаметр.
CD. Но тогда через центр О окружности проходят две прямые AB и EF, перпендикулярные CD, значит, они совпадают. Поэтому EF и AB — один и тот же диаметр.
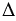 АСВ медиана СО равна половине гипотенузы, к которой она проведена. Тогда ОА = ОВ = ОС, т.е. С лежит на окружности с центром О радиуса ОА.
АСВ медиана СО равна половине гипотенузы, к которой она проведена. Тогда ОА = ОВ = ОС, т.е. С лежит на окружности с центром О радиуса ОА. ACB медиана CO равна половине стороны, к которой она проведена, поэтому угол АСВ прямой.
ACB медиана CO равна половине стороны, к которой она проведена, поэтому угол АСВ прямой.Вернуться к содержанию учебника