Номер 307 - ГДЗ Алгебра 8 класс. Мерзляк, Полонский. Учебник. Страница 74
Вернуться к содержанию учебника
Упражнения § 9. Страница 74
Вопрос
Функция задана формулой 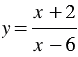 . Какова область определения данной функции? Заполните таблицу, вычислив соответствующие значения функции.
. Какова область определения данной функции? Заполните таблицу, вычислив соответствующие значения функции.
 |
-3 | -2 | -1 | 0 | 1 | 2 | 3 |
 |
Подсказка
Вспомните:
- Что называют функцией, ее область определения.
- Деление и дроби.
- Деление рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Сокращение дробей.
- Неправильные дроби.
- Деление с остатком.
- Смешанные числа.
Ответ

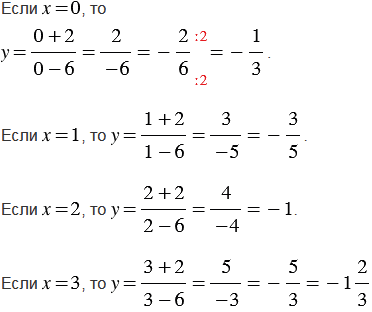
Пояснения:
Функцией называют правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной. Как правило, независимую переменную обозначают буквой 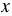 , зависимую - буквой
, зависимую - буквой 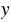 . Независимую переменную еще называют аргументом функции.
. Независимую переменную еще называют аргументом функции.
Все значения, которые принимает независимая переменная (аргумент), образуют область определения функции. Значит, область определения функции 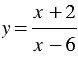 составляют все числа, кроме
составляют все числа, кроме 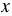 = 6, так как при
= 6, так как при 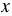 = 6 знаменатель рассматриваемой функции обращается в ноль, а на ноль делить нельзя.
= 6 знаменатель рассматриваемой функции обращается в ноль, а на ноль делить нельзя.
Чтобы найти значение функции 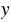 при заданном значении аргумента
при заданном значении аргумента 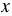 , нужно в формулу, которая задает рассматриваемую функцию, в данном случае это формула
, нужно в формулу, которая задает рассматриваемую функцию, в данном случае это формула 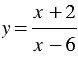 , вместо
, вместо 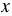 подставить числовое значение данное в условии и выполнить вычисления. При выполнении вычислений учитываем то, что, если числитель больше знаменателя, то дробь можно заменить делением (числитель делим на знаменатель). Если же дробь неправильная (числитель больше знаменателя) и числитель не делится нацело на знаменатель, то рассматриваемую неправильную дробь нужно преобразовать в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части. Если полученная дробь сократимая, то ее нужно сократить (сокращение дроби - это деление числителя и знаменателя данной дроби на их общий делитель, отличный от 1).
подставить числовое значение данное в условии и выполнить вычисления. При выполнении вычислений учитываем то, что, если числитель больше знаменателя, то дробь можно заменить делением (числитель делим на знаменатель). Если же дробь неправильная (числитель больше знаменателя) и числитель не делится нацело на знаменатель, то рассматриваемую неправильную дробь нужно преобразовать в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части. Если полученная дробь сократимая, то ее нужно сократить (сокращение дроби - это деление числителя и знаменателя данной дроби на их общий делитель, отличный от 1).
Также при вычислениях помним следующие правила:
1) чтобы сложить два числа с разными знаками, надо: найти модули слагаемых; из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем;
2) чтобы сложить два отрицательных числа, надо: найти модули слагаемых; сложить модули слагаемых; перед полученным числом поставить знак "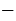 ";
";
3) сумма двух противоположных чисел равна нулю, можно записать так: 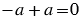 ;
;
4) чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: 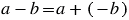 ;
;
5) чтобы найти частное двух отрицательных чисел, надо разделить модуль делимого на модуль делителя;
6) чтобы найти частное двух чисел с разными знаками, надо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак " ".
".
Вернуться к содержанию учебника