Задание 403 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№403 учебника 2013-2022 (стр. 112):
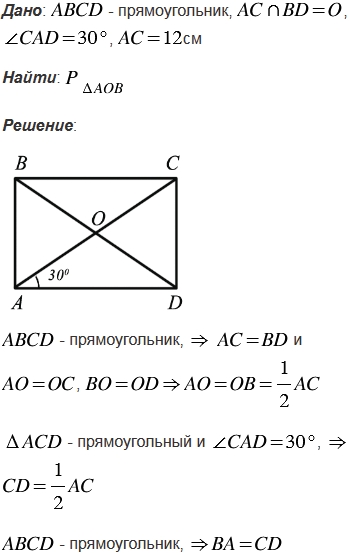
В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если 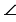 CAD = 300, АС = 12 см.
CAD = 300, АС = 12 см.
№403 учебника 2023-2024 (стр. 115):
 , параллельны.
, параллельны.Подсказка
№403 учебника 2013-2022 (стр. 112):
Вспомните:
- Какой треугольник называется прямоугольным.
- Свойства прямоугольного треугольника.
- Что такое параллелограмм.
- Что такое прямоугольник.
№403 учебника 2023-2024 (стр. 115):
Вспомните:
- Какие фигуры называют симметричными относительно прямой.
- Какие прямые называют параллельными.
Ответ
№403 учебника 2013-2022 (стр. 112):


№403 учебника 2023-2024 (стр. 115):
Дано: прямые с1 и b1 симметричны прямым с и b относительно прямой  , с
, с 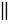 b.
b.
Доказать: с1 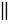 b1
b1
Доказательство:
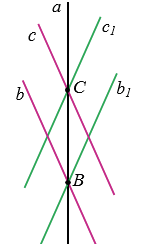
Докажем от противного.
Предположим, что с1 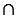 b1 = О1, при этом прямые с1 и b1 симметричны прямым с и b относительно прямой
b1 = О1, при этом прямые с1 и b1 симметричны прямым с и b относительно прямой 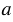 , тогда в таком случае должна существовать точка О такая, что с
, тогда в таком случае должна существовать точка О такая, что с 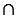 b = О, что противоречит условию с
b = О, что противоречит условию с 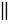 b,
b, 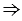 с1
с1 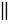 b1. Что и требовалось доказать.
b1. Что и требовалось доказать.
Пояснения:
Доказательство проводим от противного (то есть предполагаем обратное тому, что нужно доказать).
Предположим, что прямые с1 и b1, симметричные прямым с и b относительно прямой 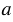 , пересекаются в точке О, то есть с1
, пересекаются в точке О, то есть с1 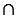 b1 = О1. Но мы знаем, что две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно, следовательно, должна существовать такая точка О, в которой будут пересекаться прямые с и b, то есть с
b1 = О1. Но мы знаем, что две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно, следовательно, должна существовать такая точка О, в которой будут пересекаться прямые с и b, то есть с 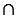 b = О, а по условию с
b = О, а по условию с 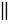 b ( параллельные прямые - это две прямые, которые не пересекаются в какую бы сторону их не продлили). Получили противоречие, значит, наше предположение неверно и с 1
b ( параллельные прямые - это две прямые, которые не пересекаются в какую бы сторону их не продлили). Получили противоречие, значит, наше предположение неверно и с 1 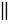 b1. Что и требовалось доказать.
b1. Что и требовалось доказать.
Вернуться к содержанию учебника