Страница 105 - ГДЗ Математика 3 класс. Моро, Бантова. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
9. Из двух листов цветной бумаги можно сделать для украшения ёлки 6 одинаковых фонариков. Сколько таких фонариков можно сделать из восьми таких же листов бумаги?
Подсказка
Повтори, как оформить краткую запись задачи таблицей.
Ответ
Вариант ответа #1:

Пояснение
Выражение для решения задачи:
8 • (6 : 2) = 24 (ф.)
Вариант ответа #2:
Решение
1) 6 : 2 = 3 (ф.)
2) 8 • 3 = 24 (ф.)
Ответ: 24 фонарика можно сделать.
Пояснение
|
Расход бумаги на 1 фонарик |
Количество фонариков |
Общее количество листов бумаги |
|
? (одинаковый)
|
6 шт. |
2 л. |
|
? шт. |
8 л. |
1) 6 : 2 = 3 (ф.) — можно сделать из одного листа бумаги
2) 8 • 3 = 24 (ф.) — можно сделать из восьми листов бумаги
Ответ: 24 фонарика можно сделать.
Вопрос
10. 1) 24 л фруктового сока разлили в 8 банок поровну. Сколько надо таких банок, чтобы разлить 18 л сока? 21 л сока?
2) Составь задачу по выражению
12 : (15 : 5).
Подсказка
Повтори, как оформить краткую запись задачи таблицей.
Ответ
Вариант ответа #1:
1)

2)

Пояснение
1) Выражения для решения задачи:
18 : (24 : 8) = 6 (б.)
21 : (24 : 8) = 7 (б.)
2)

Вариант ответа #2:
Решение
Задание 1:
1) 24: 8 = 3 (л)
2) 18 : 3 = 6 (б.)
3) 21 : 3 = 7 (б.)
Ответ: 6 банок и 7 банок.
Задание 2:
Для засолки 15 кг помидоров маме понадобилось 5 банок. Сколько банок потребуется маме для засолки 12 кг помидоров?
Пояснение
Задание 1:
|
Вместимость 1 банки |
Количество банок |
Общее количество сока |
|
? (одинаковый) |
8 шт. |
24 л |
|
? шт. |
18 л |
|
|
? шт. |
21 л |
1) 24: 8 = 3 (л) — сока в одной банке.
2) 18 : 3 = 6 (б.) — нужно для 18 л сока.
3) 21 : 3 = 7 (б.) — нужно для 21 л сока.
Ответ: 6 банок и 7 банок.
Задание 2:
|
Вместимость 1 банки |
Количество банок |
Общее количество помидоров |
|
? (одинаковый)
|
5 шт. |
15 кг |
|
? шт. |
12 кг |
12 : (15 : 5) = 12 : 3 = 4 (б.)
Ответ: маме потребуется 4 банки.
Вопрос
11.
| 45 : 5 • 9 | 70 - 6 • 7 - 6 |
| 56 : 7 • 3 | 26 + 8 - 4 • 7 |
| 32 : 4 • 8 | 35 : 5 + 2 • 7 |
| 54 : 9 • 4 | 8 • 9 - 8 • 5 |
| 8 • 3 : 6 | (44 - 8) : 4 |
| 6 • 6 : 9 | 9 • (10 - 2) |
| 2 • 9 : 3 | (8 + 6) : 7 |
| 9 • 4 : 6 | 7 • (10 - 9) |
Подсказка
Вспомни порядок выполнения действий при нахождении значения числовых выражений со скобками и без них.
Ответ
Вариант ответа #1:
Решение

Пояснение
|
45 : 5 • 9 = 81 1) 45 : 5 = 9 2) 9 • 9 = 81 |
70 - 6 • 7 - 6 = 22 1) 6 • 7 = 42 2) 70 - 4 2 = 28 3) 28 - 6 = 22 |
|
56 : 7 • 3 = 24 1) 56 : 7 = 8 2) 8 • 3 = 24 |
26 + 8 - 4 • 7 = 6 1) 4 • 7 = 28 2) 26 + 8 = 34 3) 34 - 28 = 6 |
|
32 : 4 • 8 = 64 1) 32 : 4 = 8 2) 8 • 8 = 64 |
35 : 5 + 2 • 7 = 21 1) 35 : 5 = 7 2) 2 • 7 = 14 3) 7 + 14 = 21 |
|
54 : 9 • 4 = 24 1) 54 : 9 = 6 2) 6 • 4 = 24 |
8 • 9 - 8 • 5 = 32 1) 8 • 9 = 72 2) 8 • 5 = 40 3) 72 - 40 = 32 |
|
8 • 3 : 6 = 4 1) 8 • 3 = 24 2) 24 : 6 = 4 |
(44 - 8) : 4 = 9 1) 44 - 8 = 36 2) 36 : 4 = 9 |
|
6 • 6 : 9 = 4 1) 6 • 6 = 36 2) 36 : 9 = 4 |
9 • (10 - 2) = 72 1) 10 - 2 = 8 2) 9 • 8 = 72 |
|
2 • 9 : 3 = 6 1) 2 • 9 = 18 2) 18 : 3 = 6 |
(8 + 6) : 7 = 2 1) 8 + 6 = 14 2) 14 : 7 = 2 |
|
9 • 4 : 6 = 6 1) 9 • 4 = 36 2) 36 : 6 = 6 |
7 • (10 - 9) = 7 1) 10 - 9 = 1 2) 7 • 1 = 7 |
Вариант ответа #2:
| 45 : 5 • 9 = 81 | 70 - 6 • 7 - 6 = 22 |
| 56 : 7 • 3 = 24 | 26 + 8 - 4 • 7 = 6 |
| 32 : 4 • 8 = 64 | 35 : 5 + 2 • 7 = 21 |
| 54 : 9 • 4 = 24 | 8 • 9 - 8 • 5 = 32 |
| 8 • 3 : 6 = 4 | (44 - 8) : 4 = 9 |
| 6 • 6 : 9 = 4 | 9 • (10 - 2) = 72 |
| 2 • 9 : 3 = 6 | (8 + 6) : 7 = 2 |
| 9 • 4 : 6 = 6 | 7 • (10 - 9) = 7 |
Пояснение
|
45 : 5 • 9 = 9 • 9 = 81 |
70 - 6 • 7 - 6 = 70 - 42 - 6 = 28 - 6 = 22 |
|
56 : 7 • 3 = 8 • 3 = 24 |
26 + 8 - 4 • 7 = 26 + 8 - 28 = 34 - 28 = 6 |
|
32 : 4 • 8 = 8 • 8 = 64 |
35 : 5 + 2 • 7 = 7 + 14 = 21 |
|
54 : 9 • 4 = 6 • 4 = 24 |
8 • 9 - 8 • 5 = 72 - 40 = 32 |
|
8 • 3 : 6 = 24 : 6 = 4 |
(44 - 8) : 4 = 36 : 4 = 9 |
|
6 • 6 : 9 = 36 : 9 = 4 |
9 • (10 - 2) = 9 • 8 = 72 |
|
2 • 9 : 3 = 18 : 3 = 6 |
(8 + 6) : 7 = 14 : 7 = 2 |
|
9 • 4 : 6 = 36 : 6 = 6 |
7 • (10 - 9) = 7 • 1 = 7 |
Вопрос
Выберите год учебника
Стр. 105 учебника 2023-2025:
12. 1) Запиши все двузначные числа, которые меньше 20. Увеличь каждое из них на 10.
2) Запиши все однозначные числа, которые больше 5. Увеличь каждое из них в 7 раз.
Стр. 105 учебника 2011-2022:
12. 1) Запиши все двузначные числа, которые меньше 20. Увеличь каждое из них на 10.
2) Запиши все однозначные числа, которые больше 6. Уменьши каждое из них на 7.
Подсказка
Ответ
Стр. 105 учебника 2023-2025:
Решение
1) 10, 11, 12, 13, 14, 15, 16, 17, 18, 19.
| 10 + 10 = 20 | 15 + 10 = 25 |
| 11 + 10 = 21 | 16 + 10 = 26 |
| 12 + 10 = 22 | 17 + 10 = 27 |
| 13 + 10 = 23 | 18 + 10 = 28 |
| 14 + 10 = 24 | 19 + 10 = 29 |
2) 6, 7, 8, 9.
| 6 • 7 = 42 | 8 • 7 = 56 |
| 7 • 7 = 49 | 9 • 7 = 63 |
Пояснение
Чтобы увеличить число в n раз, надо его умножить на n.
Стр. 105 учебника 2011-2022:
Вариант ответа #1:
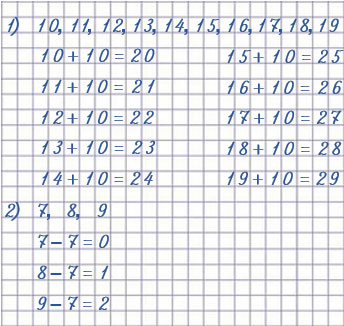
Вариант ответа #2:
Задание 1:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19
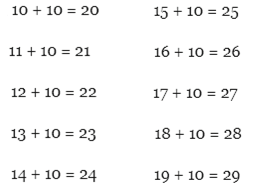
Задание 2:
7, 8, 9
7 - 7 = 0
8 - 7 = 1
9 - 7 = 1
Вопрос
13. Используя каждую пару выражений, составь и запиши верное равенство или неравенство.
|
48 + 7 63 - 8 |
3 • 7 7 + 7 + 7 |
|
70 - (13 + 22) 70 - 13 + 22 |
12 • 7 7 • 12 |
Подсказка
Повтори, чем равенство отличается от неравенства.
Также помним, от перестановки мест множителей произведение не меняется.
Ответ
Вариант ответа #1:
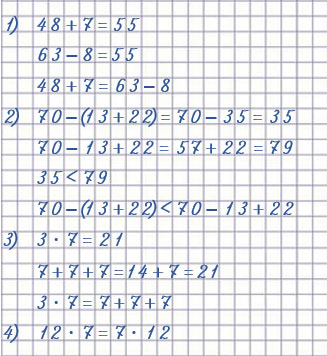
Вариант ответа #2:
Решение
| 70 - (13 + 22) < 70 - 13 + 22 |
| 7 + 7 + 7 = 3 • 7 |
| 48 + 7 = 63 - 8 |
| 12 • 7 = 7 • 12 |
Пояснение
|
70 - (13 + 22) < 70 - 13 + 22 70 - 45 < 57 + 22 25 < 79 |
|
7 + 7 + 7 = 3 • 7 21 = 21 |
|
48 + 7 = 63 - 8 55 = 55 |
|
12 • 7 = 7 • 12 перестановка мест множителей |
Вопрос
Выберите год учебника
Стр. 105 учебника 2023-2025:
14. 1) Увеличь на 8 числа: 9; 12; 18; 34; 50; 75; 83; 62.
2) Увеличь в 8 раз числа: 9; 5; 8; 4; 7; 6; 10; 1.
Стр. 105 учебника 2011-2022:
14. 1) Увеличь на 8 числа: 9; 12; 18; 34; 50; 75; 83; 62.
2) Увеличь в 8 раз числа: 9; 5; 8; 4; 7; 6; 10; 1.
Подсказка
Ответ
Стр. 105 учебника 2023-2025:
Решение
1)
| 9 - 8 = 1 | 50 - 8 = 42 |
| 12 - 8 = 4 | 75 - 8 = 67 |
| 18 - 8 = 10 | 83 - 8 = 75 |
| 34 - 8 = 26 | 62 - 8 = 54 |
2)
| 8 : 8 = 1 | 56 : 8 = 7 |
| 24 : 8 = 3 | 72 : 8 = 9 |
| 16 : 8 = 2 | 32 : 8 = 4 |
Пояснение
Во сколько раз больше? Большее число разделить на меньшее. Деление.
Стр. 105 учебника 2011-2022:
Вариант ответа #1:

Вариант ответа #2:
Задание 1:

Задание 2:

Вопрос
15. 1) Найди длину стороны квадрата ABCD, периметр которого 8 см. Начерти его и вычисли площадь.
2) Начерти прямоугольник, площадь которого равна площади квадрата ABCD, а длина одной из сторон прямоугольника 1 см.
Подсказка
Периметр многоугольника - это сумма длин всех его сторон. У квадрата все стороны равны, поэтому мы можем длину умножить на 4 и вычислить периметр.
Площадь прямоугольника равна произведению его длины и ширины. У квадрата длина равна ширине.
Ответ
Вариант ответа #1:
Решение
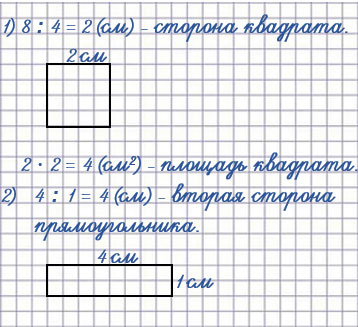
Пояснение
Задание 1:
В задаче известно, что периметр квадрата равен 8 см. Мы знаем, что периметр квадрата это сумма всех его четырех сторон. Чтобы найти сторону квадрата, нужно его периметр разделить на 4. Тогда сторона квадрат , который нам нужно начертить равна:
8 : 4 = 2 (см)
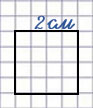
Чтобы найти площадь квадрата, нужно умножить его длину на ширину, при этом учитываем то, что длина и ширина у квадрата одинаковые. Значит, площадь квадрата, который мы начертили, равна:
2 • 2 = 4 (см2)
Задание 2:
В задаче известно, что площадь прямоугольника равна площади квадрата, который мы построили в первом задании, то есть площадь прямоугольника равна 4 см². Мы знаем, что площадь прямоугольника это произведение его длины и ширины. По условию задачи ширина равна 1 см. Чтобы найти длину прямоугольника, нужно его площадь разделить на ширину. Значит, длина прямоугольника равна:
4 : 1 = 4 (см)
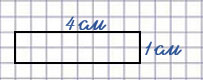
Вариант ответа #2:
Решение
Задание 1:
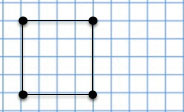
Сторона квадрата 2 см.
Площадь квадрата 4 см2.
Задание 2:

Вторая сторона прямоугольника 4 см.
Пояснение
Задание 1:
В задаче известно, что периметр квадрата равен 8 см. Мы знаем, что периметр квадрата это сумма всех его четырех сторон. Чтобы найти сторону квадрата, нужно его периметр разделить на 4.

Задание 2:
В задаче известно, что площадь прямоугольника равна площади квадрата, который мы построили в первом задании, то есть площадь прямоугольника равна 4 см². Мы знаем, что площадь прямоугольника это произведение его длины и ширины. По условию задачи ширина равна 1 см. Чтобы найти длину прямоугольника, нужно его площадь разделить на ширину.

Вопрос

16. 72 • 0  72 • 1
72 • 1
64 : 1  63 • 1
63 • 1
18 : 18  18 : 1
18 : 1
0 • 32  32 • 0
32 • 0
Подсказка
Если число разделить на 1, получится то же самое число. Если число умножить на 1, получится то же самое число.
Если число разделить само на себя, то получится 1.
Если 0 умножить на число, получится 0. Если число умножить на 0, получится 0.
Ответ
Вариант ответа #1:
Решение

Пояснение
|
72 • 0 < 72 • 1 72 • 0 = 0 72 • 1 = 72 0 < 72 |
18 : 18 < 18 : 1 18 : 18 = 1 18 : 1 = 18 1 < 18 |
|
64 : 1 > 63 • 1 64 : 1 = 64 63 • 1 = 63 64 > 63 |
0 • 32 = 32 • 0 = 0 |
Вариант ответа #2:
| 72 • 0 < 72 • 1 | 18 : 18 < 18 : 1 |
| 64 : 1 > 63 • 1 | 0 • 32 = 32 • 0 |
Пояснение
|
72 • 0 < 72 • 1 0 < 72 |
18 : 18 < 18 : 1 1 < 18 |
|
64 : 1 > 63 • 1 64 > 63 |
0 • 32 = 32 • 0 0 = 0 |
Вопрос
Цепочка:

Подсказка
Внимательно рассмотри цепочку и выполни действия.
Вопрос
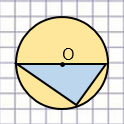
Начерти:
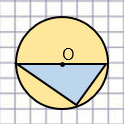
Подсказка
Отрезок, который соединяет центр окружности с какой-нибудь её точкой, называется радиусом окружности.
Ответ
Вернуться к содержанию учебника