Комбинаторные задачи

Комбинаторика (от латинского слова combinare, означающего №соединять", "сочетать") - это область математики, которая изучает способы выбора, расположения, сочетания различных объектов. Решение задач в данном разделе математики требует рассмотрения и подсчёта всех возможных комбинаций (отсюда название комбинаторные задачи). Решая эти задачи, обычно надо отвечать на вопрос "Сколькими способами...?" или "Сколько вариантов..?"

Задача: Нам даны фигуры: треугольник, овал и прямоугольник . Необходимо построить пирамидку, состоящую из трех разных фигур. Сколькими способами это можно сделать?

Метод перебора

Данный метод удобен при небольшом числе вариантов. Решение в данном случае происходит путём перебора всех возможных вариантов. При этом очень важно выбрать правильный вариант перебора - логику перебора.

Воспользуемся методом перебора: Пусть в основании пирамидки находится прямоугольник, тогда возможны варианты построения: прямоугольник - овал - треугольник и прямоугольник - треугольник - овал.

Теперь в основании положим овал, тогда возможны варианты построения: овал - прямоугольник  - треугольник и овал - треугольник - прямоугольник.

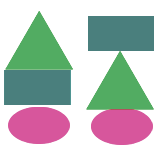
Теперь в основании положим треугольник, тогда возможны варианты построения: треугольник - прямоугольник - овал и треугольник - овал - прямоугольник.

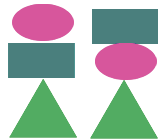
Итак, мы получили шесть возможных вариантов:

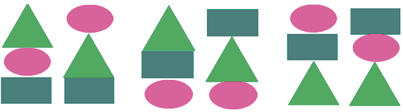
Ответ: 6 способов.

При решении данной задачи мы изображали фигуры, но для упрощения решения можно использовать кодирование. Данный прием позволяет заметить фигуры, например, первыми буквами их названия, то есть овал обозначаем буквой  О, треугольник - Т, прямоугольник - П. Тогда решение будет выглядеть так:

Т  О  Т  П  О  П

О  Т  П  Т  П  О

П  П  О  О Т   Т

Дерево возможных вариантов

Данный метод заключается в построении схемы, которая и называется деревом возможных вариантов. Данная схема действительно похожа на перевернутое дерево, "корень" которого обозначается "*". Построим данную схему для нашей задачи:  Для этого от "корня" проведем  три "ветки" - отрезки, на концах которых подпишем варианты фигур, которые мы можем взять за основание. Далее от каждой фигуры проводим такое количество "веток", которое будет соответствовать числу вариантов фигур на втором месте, в нашем случае по две "ветки" от каждой фигуры. Затем от каждой фигуры, стоящей на втором месте,  проводим такое число "веток", которое будет соответствовать числу вариантов фигур на третьем месте, в нашем случае по одной "ветке" от каждой фигуры. Тогда имеем следующее дерево возможных вариантов:

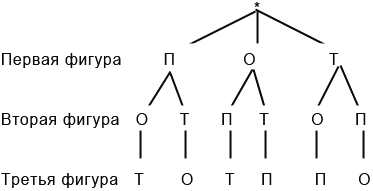
Метод отрезков

Данный метод используется только для составления всевозможных пар. Например, рассмотрим прямую, на которой обозначены точки A, B, C, D, F:

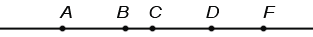
Необходимо ответить  на вопрос: " Сколько отрезков изображено на рисунке?". Мы знаем, что отрезок обозначается двумя буквами, значит, для ответа на вопрос необходимо перебрать всевозможные пары букв. Это можно сделать при помощи следующей схемы: Отметим точки так, чтобы никакие 3 не лежали на одной прямой:

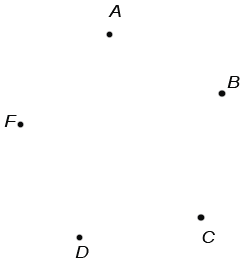
Соединим  данные точки отрезками между собой. Число отрезков будет числом вариантов, то есть числом отрезков, изображенных на рисунке:

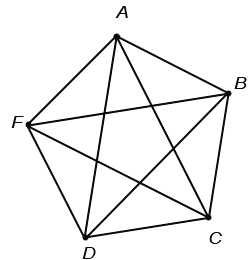
Итак, мы получили 10 отрезков, соединяющих точки.

Ответ: На рисунке 10 отрезков.