Случайные события. Вероятность случайного события
Событие, которое может произойти, а может не произойти в процессе наблюдения или эксперимента, называют случайным событием. Так, например, пошел дождь - событие, которое может произойти или не произойти, т.е. это событие является случайным.
Вероятности случайных событий - это величины, которые можно сравнивать. Но нужно договориться, каким образом количественно оценивать возможность появления того или иного случайного события. Закономерности случайных событий изучает специальный раздел математики, который теорией вероятностей.
Если событие при рассматриваемых условиях происходит всегда, то оно называется достоверным. Вероятность появления достоверного события равна 1. Так, например, событие "Лето составляет 92 дня" является достоверным.
Если событие при рассматриваемых условиях не происходит никогда, то оно называется невозможным. Вероятность появления невозможного события равна 0. Так, например, событие "После декабря наступит май" является невозможным.
Вероятность случайного события может быть любым числом от 0 до 1.
Если все исходы эксперимента имеют равные шансы, то они называются равновероятными (или равновозможными). Так, например, при подбрасывании монеты может выпасть "орел", а может - "решка", вероятность каждого из этих событий равна 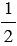 . Не все события равновероятны. Например, событие "В школе на урок прозвенит звонок" более вероятно, чем событие "В школе на урок не прозвенит звонок". Вероятность наступления зависит от условий, в которых оно рассматривается.
. Не все события равновероятны. Например, событие "В школе на урок прозвенит звонок" более вероятно, чем событие "В школе на урок не прозвенит звонок". Вероятность наступления зависит от условий, в которых оно рассматривается.
Различные испытания, опыты, наблюдения, результаты которых предсказать нельзя - это примеры экспериментов со случайными исходами (результатами).
Определение вероятности:
Если эксперимент заканчивается одним из 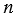 равновероятных исходов, из которых равновероятных исходов, из которых 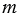 являются благоприятными для наступления данного события, то вероятность этого события равна являются благоприятными для наступления данного события, то вероятность этого события равна 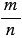 . . |
Вероятность события обозначается буквой 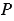 . Так, например, вероятность наступления события А записывают так:
. Так, например, вероятность наступления события А записывают так: 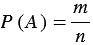 , где
, где 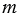 - благоприятное число исходов,
- благоприятное число исходов, 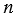 - общее число исходов.
- общее число исходов.
Пример: Какова вероятность того, что при бросании игрального кубика выпадет: 1) менее трех очков; 2) более шести очков; 3) не более шести очков.
Решение:
1) При бросании кубика может произойти 6 равновероятных исходов: выпадет 1, 2, 3, 4, 5 или 6 очков. Из них благоприятными являются два исхода: выпадет 1 очко или выпадет 2 очка, т.к. 1 меньше 3 и 2 меньше 3. Поэтому искомая вероятность 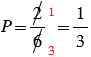 .
.
2) При бросании кубика может произойти 6 равновероятных исходов: выпадет 1, 2, 3, 4, 5 или 6 очков. Из них нет ни одного благоприятного исхода, т.к. более шести очков на кубике выпасть не может, значит, рассматриваемое событие является невозможным и его вероятность 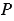 = 0.
= 0.
3) При бросании кубика может произойти 6 равновероятных исходов: выпадет 1, 2, 3, 4, 5 или 6 очков. Из них все исходы являются благоприятными, т.к. любое из чисел 1, 2, 3, 4, 5, 7 меньше 7, значит, рассматриваемое событие является достоверным и его вероятность 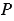 = 1.
= 1.
Ответ: 1) 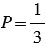 ; 2)
; 2) 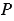 = 0; 3)
= 0; 3) 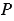 = 1.
= 1.
Советуем посмотреть:
Правило встречается в следующих упражнениях:
6 класс
Номер 802, Мерзляк, Полонский, Якир, Учебник
Номер 806, Мерзляк, Полонский, Якир, Учебник
Номер 811, Мерзляк, Полонский, Якир, Учебник
Номер 812, Мерзляк, Полонский, Якир, Учебник
Номер 816, Мерзляк, Полонский, Якир, Учебник
Номер 822, Мерзляк, Полонский, Якир, Учебник
Номер 824, Мерзляк, Полонский, Якир, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 5, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
7 класс
Номер 388, Мерзляк, Полонский, Якир, Учебник
Номер 473, Мерзляк, Полонский, Якир, Учебник
Номер 618, Мерзляк, Полонский, Якир, Учебник
Номер 944, Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 436, Мерзляк, Полонский, Якир, Учебник