Упражнение 183 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 68
Вернуться к содержанию учебника
Вопрос
Постройте в одной системе координат графики функций \(y=\dfrac{1}{3}x^{2}\) и \(y=-\dfrac{1}{3}x^{2}\). Найдите промежутки возрастания и убывания для каждой функции.
Подсказка
Вспомните:
- Свойства функций.
- Квадратичную функцию, ее график.
- Координаты точки на координатной плоскости.
- Степень с натуральным показателем.
Ответ
1) \(y=\dfrac{1}{3}x^{2}\) - парабола, ветви направлены вверх.
| \(x\) | \(-6\) | \(-3\) | \(-1\) | \(0\) | \(1\) | \(3\) | \(6\) |
| \(y\) | \(12\) | \(3\) | \(\frac13\) | \(0\) | \(\frac13\) | \(3\) | \(12\) |
2) \(y=-\dfrac{1}{3}x^{2}\) - парабола, ветви направлены вниз.
| \(x\) | \(-6\) | \(-3\) | \(-1\) | \(0\) | \(1\) | \(3\) | \(6\) |
| \(y\) | \(-12\) | \(-3\) | \(-\frac13\) | \(0\) | \(-\frac13\) | \(-3\) | -12 |
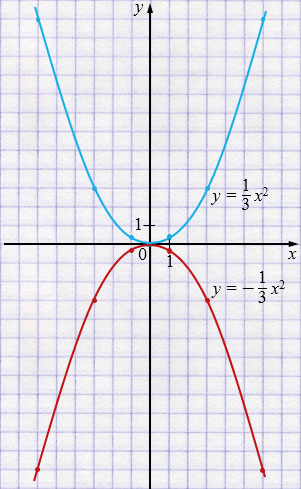
Функция \(y=\dfrac{1}{3}x^{2}\) убывает на \((-\infty, 0)\), возрастает на \((0, +\infty)\).
Функция \(y=-\dfrac{1}{3}x^{2}\) возрастает на \((-\infty, 0)\), убывает на \((0, +\infty)\).
Пояснения:
Обе функции — параболы вида \(y=ax^{2}\). При \(a>0\) ветви параболы направлены вверх, при \(a<0\) — вниз.
Для параболы вершина отделяет участки возрастания и убывания. Если ветви вверх, то слева функция убывает, справа возрастает. Если ветви вниз — наоборот.
Коэффициент \(\dfrac{1}{3}\) делает параболы более «плоскими» по сравнению со стандартной \(y=x^{2}\).
Вернуться к содержанию учебника