Упражнение 1035 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1035 учебника 2023-2025 (стр. 229):
Верно ли, что:
а) \((-5; 5) \cap (-3; 2) = (-3; 2)\);
б) \((4; 11) \cup (0; 6) = (4; 6)\);
в) \((-\infty; 4) \cup (1; +\infty) = (-\infty; +\infty)\);
г) \((-\infty; 2) \cap (-2; +\infty) = (-2; 2)\)?
№1035 учебника 2013-2022 (стр. 230):
Учащимся восьмых классов школ некоторого города была предложена контрольная работа по алгебре, содержащая 6 заданий. При подведении итогов составили таблицу, в которой указали число учащихся, верно выполнивших одно, два, три и т. д. задания.
| Число выполненных заданий | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Число учащихся | – | 27 | 53 | 87 | 223 | 146 | 89 |
Пользуясь этой таблицей, составьте таблицу относительных частот (с точностью до 1%).
Подсказка
№1035 учебника 2023-2025 (стр. 229):
Вспомните:
№1035 учебника 2013-2022 (стр. 230):
Вспомните:
Ответ
№1035 учебника 2023-2025 (стр. 229):
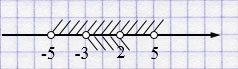
а) \((-5; 5) \cap (-3; 2) = (-3; 2)\) - верно.
б) \((4; 11) \cup (0; 6) = (4; 6)\) - неверно.
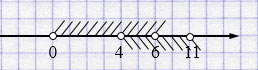
\((4; 11) \cup (0; 6) = (0; 11)\)
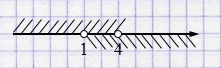
в) \((-\infty; 4) \cup (1; +\infty) = (-\infty; +\infty)\) - верно.
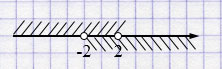
г) \((-\infty; 2) \cap (-2; +\infty) = (-2; 2)\) - верно.
Пояснения:
Пересечение двух промежутков \(\cap\) — это множество чисел, которые принадлежат и первому, и второму промежутку одновременно.
Объединение двух промежутков \(\cup\) — это множество чисел, которые принадлежат хотя бы одному из них.
— Если один промежуток полностью входит в другой, их пересечение равно меньшему из них.
— Если промежутки перекрываются, объединение образует непрерывный промежуток от минимального до максимального значения.
№1035 учебника 2013-2022 (стр. 230):
\( 27 + 53 + 87 + 223 + 146 + 89 = 625\) - общее число учащихся.
Теперь вычислим относительные частоты (в процентах):
\( \frac{27}{625}\cdot100\%\approx 4\%,\)
\(\frac{53}{625}\cdot100\%\approx 8\%,\)
\(\frac{87}{625}\cdot100\%\approx 14\%,\)
\(\frac{223}{625}\cdot100\%\approx 36\%,\)
\(\frac{146}{625}\cdot100\%\approx 23\%,\)
\(\frac{89}{625}\cdot100\%\approx 14\%. \)
| Число выполненных заданий | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Относительная частота | 0% | 4% | 8% | 14% | 36% | 23% | 14% |
Пояснения:
Относительная частота показывает, какая доля всех наблюдений соответствует данному значению признака:
\[\frac{число\; учащихся}{общее\; число\; учащихся} \cdot 100\%. \]
1. Мы нашли общее число учеников: 625.
2. Для каждого значения числа выполненных заданий разделили частоту на 625 и округлили с точностью до 1%.
3. Полученная таблица показывает распределение результатов: наиболее частый результат — выполнение 4 заданий (36% учеников).
Вернуться к содержанию учебника