Упражнение 925 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\((-3,9; 2)\) и \((-4,3; 1)\)

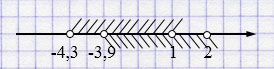
\((-3,9; 2) \cap (-4,3; 1) = (-3,9; 1)\).

Целые числа, принадлежащие \((-3,9; 1)\):

\(-3, -2, -1, 0\).

Ответ: 2. четыре числа.

Пояснения:

Пересечение двух промежутков — это множество чисел, которые принадлежат и первому, и второму промежутку одновременно.

а) \(a^2 + ab + b^2 \ge 0\)

\( a^2 + ab + b^2 =\)

\( =a^2 + 2a \cdot \frac12b + (\frac12b)^2 - (\frac12b)^2 + b^2 =\)

\( =\left(a + \frac{1}{2}b\right)^2 - \frac14b^2 + b^2 =\)

\(=\left(a + \frac{1}{2}b\right)^2 + \frac{3}{4}b^2 \ge 0\)

Что и требовалось доказать.

б) \(a^2 - ab + b^2 \ge 0\)

\( a^2 + ab + b^2 =\)

\( =a^2 - 2a \cdot \frac12b + (\frac12b)^2 - (\frac12b)^2 + b^2 =\)

\( =\left(a - \frac{1}{2}b\right)^2 - \frac14b^2 + b^2 =\)

\(=\left(a - \frac{1}{2}b\right)^2 + \frac{3}{4}b^2 \ge 0\)

Что и требовалось доказать.

Пояснения:

Метод выделения полного квадрата основан на формулах квадрата суммы и квадрата разности двух выражений:

\( (x + y)^2 = x^2 + 2xy + y^2\),

\( (x - y)^2 = x^2 - 2xy + y^2\).

В обоих случаях получили, что выражение состоит из суммы квадратов, а квадрат любого числа \( \ge 0\), поэтому всё выражение неотрицательно при любых \(a\) и \(b\). Что и требовалось доказать.