Упражнение 1152 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

\[ \begin{cases} y \le 3x + 2,\\ y \ge kx + b \end{cases} \]

а) \(k = 3\), \(b = -5\).

\[ \begin{cases} y \le 3x + 2,\\ y \ge 3x - 5 \end{cases} \]

б) \(k = -1\), \(b = -2\).

\[ \begin{cases} y \le 3x + 2,\\ y \ge -x - 2 \end{cases} \]

Ответ: а) \(k = 3\), \(b = -5\);

б) \(k = -1\), \(b = -2\).

Пояснения:

– Полоса образуется пересечением двух полуплоскостей, границами которых служат параллельные прямые.

– Угол образуется пересечением двух полуплоскостей, границами которых служат пересекающиеся прямые.

– В пункте а) при равных коэффициентах при \(x\) прямые параллельны.

– В пункте б) при разных коэффициентах при \(x\) прямые пересекаются в одной точке.

\(a x - y = 4\)

\(M(3;5)\)

\( a\cdot3 - 5 = 4 \)

\(3a = 4 + 5 \)

\(3a = 9 \)

\(a = \frac{9}{3}\)

\(a = 3 \)

\( 3x - y = 4\)

\(y = 3x - 4 \)

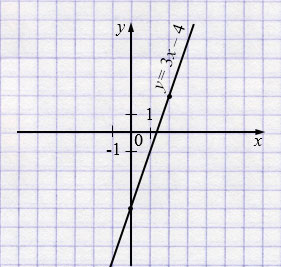
Пояснения:

– Линейная функция задаётся уравнением вида \(y = kx + b\), где \(k\) — коэффициент наклона, \(b\) — свободный член.

– Подстановка координат точки в уравнение позволяет найти неизвестный коэффициент.

– После нахождения \(a\) удобно перевести уравнение к явному виду \(y = kx + b\) для построения графика.

– Две точки определяют прямую: достаточно взять \(x=0\) и ещё одно значение, например \(x=2\).

– Полученная прямая проходит через \(M(3;5)\).