Упражнение 1048 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1048 учебника 2023-2025 (стр. 204):
Выразите из данного уравнения переменную \(y\) через \(x\); используя полученную формулу, найдите три каких-либо решения этого уравнения:
а) \(3x + 2y = 12\); б) \(5y - 2x = 1\).
№1048 учебника 2013-2022 (стр. 206):
Постройте график уравнения:
а) \(2 𝑥 − 𝑦 = 6\);
б) \(1,5 𝑥 + 2 𝑦 = 3\);
в) \(𝑥 + 6 𝑦 = 0\);
г) \(0,5 𝑦 − 𝑥 = 1\);
д) \(1,2 𝑥 = − 4,8\);
е) \(1,5 𝑦 = 6\).
Подсказка
№1048 учебника 2023-2025 (стр. 204):
Вспомните:
№1048 учебника 2013-2022 (стр. 206):
Ответ
№1048 учебника 2023-2025 (стр. 204):
а) \( 3x + 2y = 12\)
\(2y = 12 - 3x\)
\(y = \frac{12 - 3x}{2}. \)
Найдём три решения (подставим значения \(x\)):
\(x = 0\):
\(y = \frac{12 - 3 \cdot 0}{2} = \frac{12}{2} = 6\) → (0; 6)
\(x = 2\):
\(y = \frac{12 - 3 \cdot 2}{2} = \frac{6}{2} = 3\) → (2; 3)
\(x = 4\):
\(y = \frac{12 - 3 \cdot 4}{2} = \frac{0}{2} = 0\) → (4; 0)
Ответ: \(y = \frac{12 - 3x}{2};\) решения уравнения: (0; 6); (2; 3); (4; 0).
б) \( 5y - 2x = 1\)
\(5y = 1 + 2x \)
\(y = \frac{1 + 2x}{5}. \)
Найдём три решения (подставим значения \(x\)):
\(x = 0\):
\(y = \frac{1 + 0}{5} = \frac{1}{5}\) → (0; 0,2)
\(x = 2\):
\(y = \frac{1 + 4}{5} = \frac{5}{5} = 1\) → (2; 1)
\(x = 4\):
\(y = \frac{1 + 8}{5} = \frac{9}{5} = 1.8\) → (4; 1,8)
Ответ: \(y = \frac{1 + 2x}{5};\) решения уравнения: (0; 0,2); (2; 1); (4; 1,8).
Пояснения:
Как выразить \(y\) через \(x\):
Переносим все слагаемые с \(x\) в правую часть, затем делим обе стороны на коэффициент при \(y\).
а) Уравнение \(3x + 2y = 12\)
\[ 2y = 12 - 3x \Rightarrow y = \frac{12 - 3x}{2} \]
б) Уравнение \(5y - 2x = 1\)
\[ 5y = 2x + 1 \Rightarrow y = \frac{2x + 1}{5} \]
Как найти решения:
Подставляем произвольные значения переменной \(x\) и вычисляем соответствующее \(y\) по найденной формуле.
Каждая пара чисел \((x; y)\), полученная таким образом, является решением уравнения.
№1048 учебника 2013-2022 (стр. 206):
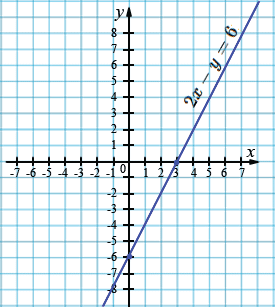
а) \(2 𝑥 − 𝑦 = 6\);
| \(x\) | 0 | 3 |
| \(y\) | -6 | 0 |
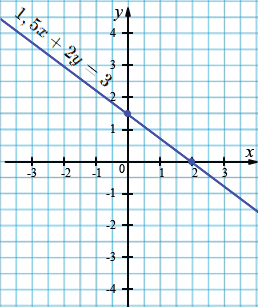
б) \(1,5 𝑥 + 2 𝑦 = 3\);
| \(x\) | 0 | 2 |
| \(y\) | 1,5 | 0 |
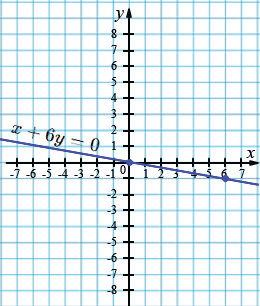
в) \(𝑥 + 6 𝑦 = 0\);
| \(x\) | 0 | 6 |
| \(y\) | 0 | -1 |
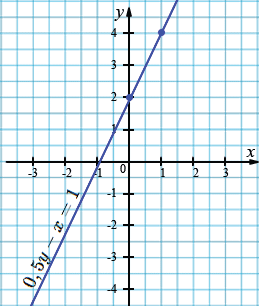
г) \(0,5 𝑦 − 𝑥 = 1\);
| \(x\) | 0 | 1 |
| \(y\) | 2 | 4 |
д) \(1,2 𝑥 = − 4,8\);
\(1,2 𝑥 + 0y= − 4,8\);
\(𝑥 = − 4,8:1,2\);
\(𝑥 = −4.\)
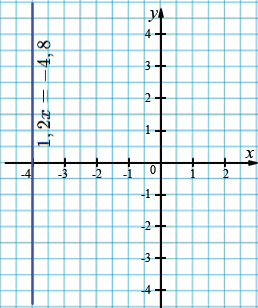
е) \(1,5 𝑦 = 6;\)
\(0x+1,5 𝑦 = 6;\)
\(𝑦 = 6:1,5;\)
\(𝑦 = 4.\)

Пояснения:
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая. Прямая определяется двумя точками, поэтому чтобы построить график линейного уравнения с двумя переменными достаточно определить координаты каких-либо двух точек прямой.
Вернуться к содержанию учебника