Упражнение 1050 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1050 учебника 2023-2025 (стр. 204):
Среди решений уравнения \(x + 2y = 18\) найдите такую пару, которая составлена из двух одинаковых чисел.
№1050 учебника 2013-2022 (стр. 206):
Постройте график уравнения:
а) \(x-y-1=0\);
б) \(3x=y+4\);
в) \(2(x-y)+3y=4\);
г) \((x+y)-(x-y)=4\).
Подсказка
№1050 учебника 2023-2025 (стр. 204):
Вспомните:
- Линейное уравнение с двумя переменными.
- Какая пара чисел является решением уравнения с двумя переменными.
№1050 учебника 2013-2022 (стр. 206):
Ответ
№1050 учебника 2023-2025 (стр. 204):
Пусть \(x = y\):
\(x + 2x = 18\)
\(3x = 18\)
\(x = 6. \)
Значит, \(y = 6\).
Решение: \((6; 6).\)
Ответ: искомая пара чисел \((6; 6).\)
Пояснения:
Нам нужно найти такие \(x\) и \(y\), чтобы они были равны, то есть \(x = y\).
Подставляем это условие в уравнение \(x + 2y = 18\), получаем:
\[ x + 2x = 18 \Rightarrow 3x = 18 \Rightarrow x = 6 \]
Следовательно, \(y = 6\), и пара одинаковых чисел, удовлетворяющая уравнению, — это \((6; 6)\).
№1050 учебника 2013-2022 (стр. 206):
а) \(x-y-1=0;\)
\(x-y=1;\)
| \(x\) | 0 | -1 |
| \(y\) | 1 | -2 |
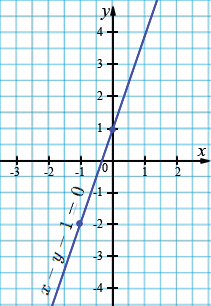
б) \(3x=y+4\);
\(3x-y=4;\)
| \(x\) | 0 | 2 |
| \(y\) | -4 | 2 |
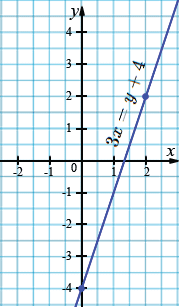
в) \(2(x-y)+3y=4;\)
\(2x-2y+3y=4;\)
\(2x+y=4;\)
| \(x\) | 0 | 2 |
| \(y\) | 4 | 0 |
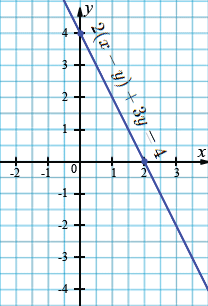
г) \((x+y)-(x-y)=4;\)
\(x+y-x+y=4;\)
\(0x+2y=4;\)
\(y=2.\)
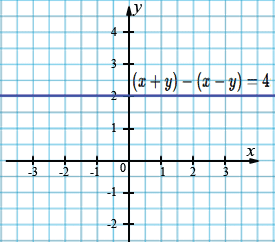
Пояснения:
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая. Прямая определяется двумя точками, поэтому чтобы построить график линейного уравнения с двумя переменными достаточно определить координаты каких-либо двух точек прямой.
Вернуться к содержанию учебника