Упражнение 624 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№624 учебника 2023-2025 (стр. 135):
Представьте выражение в виде разности одночлена и трехчлена:
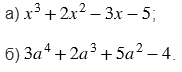
№624 учебника 2013-2022 (стр. 137):
Упростите выражение:
а) \((3a^2)^2 - a^3(1 - 5a);\)
б) \(\bigl(-\tfrac{1}{2}b\bigr)^3 - b\bigl(1 - 2b - \tfrac{1}{8}b^2\bigr);\)
в) \(x(16x - 2x^3) - (2x^2)^2;\)
г) \((0{,}2c^3)^2 - 0{,}01c^4(4c^2 - 100).\)
Подсказка
№624 учебника 2023-2025 (стр. 135):
Вспомните:
- Что называют одночленом.
- Что называют трехчленом.
- Вычитание многочленов.
- Раскрытие скобок.
№624 учебника 2013-2022 (стр. 137):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Раскрытие скобок.
- Приведение подобных слагаемых.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
Ответ
№624 учебника 2023-2025 (стр. 135):

№624 учебника 2013-2022 (стр. 137):
а) \( (3a^2)^2 - a^3(1 - 5a) = \)
\( = 9a^4 - \bigl(a^3 - 5a^4\bigr) = \)
\( = 9a^4 - a^3 + 5a^4 = 14a^4 - a^3. \)
б) \( -\tfrac{1}{8}b^3 - \bigl(b - 2b^2 - \tfrac{1}{8}b^3\bigr) = \)
\( = -\tfrac{1}{8}b^3 - b + 2b^2 + \tfrac{1}{8}b^3 = 2b^2 - b. \)
в) \( 16x^2 - 2x^4 - 4x^4 = \)
\(=16x^2 - 6x^4 = -6x^4 + 16x^2. \)
г) \( 0{,}04c^6 - \bigl(0{,}04c^6 - c^4\bigr) = \)
\( = 0{,}04c^6 - 0{,}04c^6 + c^4 = c^4. \)
Пояснения:
• Правило степени: \((ka^n)^m = k^m a^{nm}\).
• Раскрытие скобок (перед скобками знак \( "-" \) :
\(U - (V - W) = U - V + W\).
• Приведение подобных слагаемых: сложили коэффициенты при одинаковых буквенных частях и полученное значение умножили на нее.
Вернуться к содержанию учебника