Упражнение 524 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№524 учебника 2023-2025 (стр. 123):
В последовательностях записаны в порядке возрастания все натуральные числа, которые не превосходят 200, причем в первой последовательности записаны числа, кратные 6, а во второй - кратные 8:
6, 12, 18, ...;
8, 16, 24, ... .
Сколько в этих последовательностях одинаковых чисел?
№524 учебника 2013-2022 (стр. 122):
Докажите, что при любом натуральном 
дроби является натуральным числом:
Подсказка
№524 учебника 2023-2025 (стр. 123):
Вспомните:
№524 учебника 2013-2022 (стр. 122):
Вспомните:
- Степень с натуральным показателем.
- Натуральные числа.
- Деление и дроби.
- Признаки делимости на 3 и на 9.
Ответ
№524 учебника 2023-2025 (стр. 123):
6, 12, 18, 24, ...;
8, 16, 24, ... .
НОК(6; 8) = 24
Общие кратные чисел 6 и 8:
24, 48, 72, 96, 120, 144, 168, 192, ...
Ответ: в этих последовательностях 8 одинаковых чисел.
Пояснения:
Одинаковыми числами в рассматриваемых последовательностях будут общие кратные чисел 6 и 8. Чтобы найти, сколько будет таких чисел, нужно сначала определить наименьшее общее кратное чисел 6 и 8 - это число 24, а затем последовательно умножить 24 на 2, 3, 4 и т.д., чтобы получить остальные общие кратные, которые не превосходят 200 (смотри решение выше), или же можно просто 200 разделить 24, чтобы понять, какое целое число раз 24 умещается в 200, то есть
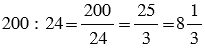, значит, в рассматриваемых последовательностях 8 одинаковых чисел, которые не превосходят 200.
№524 учебника 2013-2022 (стр. 122):
Вернуться к содержанию учебника