Упражнение 319 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 79
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№319 учебника 2023-2025 (стр. 79):
Постройте график функции, заданной формулой:

№319 учебника 2013-2022 (стр. 79):
Постройте график функции, заданной формулой:
а) \(y=-2x+1\);
б) \(y=0,2x+5\);
в) \(y=-x+4,5\);
г) \(y=x+1,5\);
д) \(y=\tfrac12x-3\);
е) \(y=-x-3,5\);
ж) \(y=-3x+4\);
з) \(y=-x+3\);
и) \(y=x-2\).
Подсказка
№319 учебника 2023-2025 (стр. 79):
№319 учебника 2013-2022 (стр. 79):
Вспомните:
- Какая зависимость называется линейной функцией.
- График линейной функции.
- Координаты на плоскости.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Умножение десятичных дробей.
- Сложение и вычитание десятичных дробей.
Ответ
№319 учебника 2023-2025 (стр. 79):






№319 учебника 2013-2022 (стр. 79):
а) \(y=-2x+1\)
| \(x\) | 1 | 0 |
| \(y\) | -1 | 1 |
Пусть \(x = 1\), тогда
\(y=-2\cdot1+1 = -1\)
Пусть \(x=0\), тогда
\(y=-2\cdot0+1 =1\)

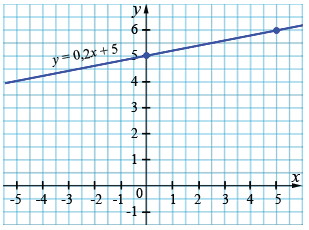
б) \(y = 0,2x + 5\)
| \(x\) | 0 | 5 |
| \(y\) | 5 | 6 |
Пусть \(x=0\), тогда
\(y = 0,2\cdot0 + 5 = 5\)
Пусть \(x=5\), тогда
\(y = 0,2\cdot5 + 5 = 1 + 5 = 6\)
в) \(y=-x+4,5\)
| \(x\) | 0,5 | -0,5 |
| \(y\) | 4 | 5 |
Пусть \(x=0,5\), тогда
\(y = -0,5 + 4,5 = 4\)
Пусть \(x=-0,5\), тогда
\(y = -(-0,5) + 4,5 = 5\)

г) \(y = x + 1,5\)
| \(x\) | 0,5 | -0,5 |
| \(y\) | 2 | 1 |
Пусть \(x=0,5\), тогда
\(y = 0,5 + 1,5 = 2\)
Пусть \(x=-0,5\), тогда
\(y = -0,5 + 1,5 = 1\).

д) \(y = \frac12x - 3\)
| \(x\) | 2 | -2 |
| \(y\) | -2 | -4 |
Пусть \(x=2\), тогда
\(y = \frac12\cdot2 - 3 = 1 - 3 = -2\)
Пусть \(x=-2\), тогда
\(y = \frac12\cdot(-2) - 3 = -1 - 3 = -4\)

е) \(y=-x-3,5\)
| \(x\) | 0,5 | -0,5 |
| \(y\) | -4 | -3 |
Пусть \(x=0,5\), тогда
\(y=-0,5-3,5 = -4\).
Пусть \(x=-0,5\), тогда
\(y=-(-0,5)-3,5 =0,5 - 3,5 = -3\).

ж) \(y=-3x+4\)
| \(x\) | 0 | 2 |
| \(y\) | 4 | -2 |
Пусть \(x=0\), тогда
\(y = -3\cdot0 + 4 = 4\).
Пусть \(x = 2\), тогда
\(y = -3\cdot2 + 4 = -6 + 4 = -2\).

з) \(y=-x+3\)
| \(x\) | 0 | 3 |
| \(y\) | 3 | 0 |
Пусть \(x = 0\), тогда
\(y= 0 + 3 = 3\).
Пусть \(x = 3\), тогда
\(y=-3+3 = 0\).

и) \(y=x-2\)
| \(x\) | 0 | 2 |
| \(y\) | -2 | 0 |
Пусть \(x = 0\), тогда
\(y = 0 - 2 = -2\).
Пусть \(x = 2\), тогда
\(y = 2 - 2 = 0\).

Пояснения:
Линейной функцией называется функция, которую можно задать формулой вида \(y=kx+b\) где \(x\) - независимая переменная, \(k\) и \(b\) - некоторые числа. Графиком линейной функции является прямая. Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки на координатной плоскости и провести через них прямую.
Вернуться к содержанию учебника