Задание 6.28 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2. Страница 103

1) а) Параллелограмм АВСD - ромб, у которого нет прямых углов.

АВ = ВС = СD = АD.

б) Параллелограмм АВСD - ромб, у которого есть прямые углы.

АВ = ВС = СD = АD.

2) Ромб, у которого углы прямые, называют квадратом.

Пояснения:

Четырехугольник, в котором противоположные стороны параллельны, называют параллелограммом.

1) а) Начертим произвольный отрезок АD.

Далее построим прямую параллельную АD. Чтобы провести прямую параллельную отрезку АD, прикладываем чертежный треугольник к отрезку АD одной из его сторон образующих прямой угол, а вдоль другой стороны чертежного треугольника, образующей прямой угол, прикладываем линейку.

Далее, не меняя положения линейки, двигаем вдоль нее чертежный треугольник на расстояние, меньшее длины отрезка АD, и проводим прямую вдоль стороны чертежного треугольника.

Учитывая то, что нам нужно построить параллелограмм, у которого все стороны равны, чертим с помощью циркуля окружность радиуса АD с центром в точке А, точку пересечения этой окружности с прямой параллельной АD обозначаем буквой В и соединяем точки А и В.

Далее чертим с помощью циркуля окружность радиуса АD с центром в точке В, точку пересечения этой окружности с прямой параллельной АD обозначаем буквой С.

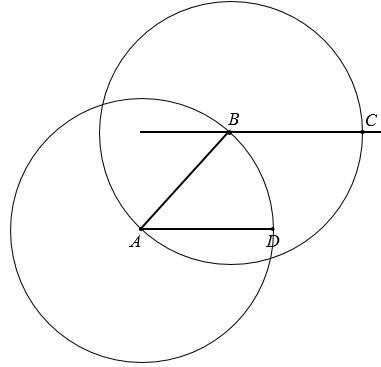
Соединяем точки С и D, стираем лишние части прямой ВС получаем параллелограмм АВСD с равными сторонами, у которого нет прямых углов, то есть получаем ромб АВСD.

б) Начертим произвольный отрезок АD.

Далее построим прямой угол с вершиной в точке А. Для этого прикладываем чертежный треугольник к прямой АD одной из его сторон, образующих прямой угол, при этом точка А должна лежать в вершине прямого угла чертежного треугольника. Чертим из точки А луч вдоль стороны чертежного треугольника.

Учитывая то, что нам нужно построить параллелограмм, у которого все стороны равны, чертим с помощью циркуля окружность радиуса АD с центром в точке А, точку пересечения этой окружности с прямой перпендикулярной АD обозначаем буквой В.

Теперь построим прямую, проходящую через точку В, параллельную АD. Чтобы провести прямую параллельную отрезку АD, проходящую через точку В, прикладываем чертежный треугольник к отрезку АD одной из его сторон образующих прямой угол, а вдоль другой стороны чертежного треугольника, образующей прямой угол, прикладываем линейку.

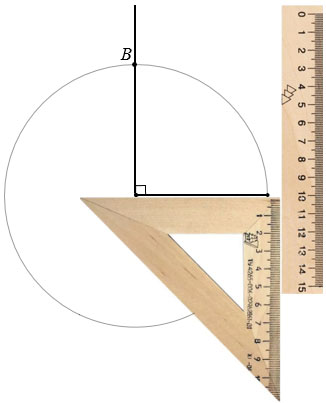
Далее, не меняя положения линейки, двигаем вдоль нее чертежный треугольник до точки В и проводим через точку В прямую вдоль стороны чертежного треугольника.

Затем чертим с помощью циркуля окружность радиуса АD с центром в точке В, точку пересечения этой окружности с прямой параллельной АD обозначаем буквой С.

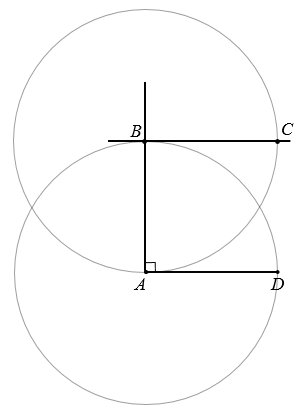
Соединяем точки С и D, стираем лишние части прямых АВ и ВС получаем параллелограмм АВСD с равными сторонами, у которого есть прямые углы, то есть получаем ромб АВСD.

Ромб АВСD является квадратом, так как ромб, у которого углы прямые, называют квадратом.