Задание 7.52 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2. Страница 152

Пусть масса контейнера без груза 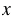т, тогда масса груза 3 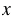т. Контейнер с грузом весит 4,4 т.

Составим уравнение:

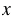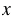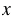+ 3 = 4,4

4 = 4,4

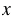= 4,4 : 4

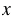= 1,1 (т) - масса контейнера без груза.

3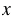 = 3 • 1,1 = 3,3 (т)

Ответ: масса груза 3,3 т.

Пояснения:

Решаем задачу с помощью уравнения.

Пусть масса контейнера без груза 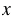т.  Масса контейнера в 3 раза меньше массы груза, то есть масса груза в 3 раза больше массы контейнера, тогда масса груза 3 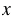т. Контейнер с грузом весит 4,4 т. Получается, можем составить следующее уравнение:

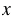+ 3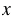 = 4,4.

В левой части полученного уравнения применяем распределительное свойство умножения относительно сложения, получим:

(1 + 3)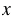 = 4,4 или, выполнив сложение,

4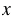 = 4,4.

Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:

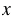= 4,4 : 4,

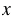= 1,1.

Значит, масса контейнера без груза равна 1,1 т.

Тогда масса груза:

3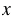 = 3 • 1,1 = 3,3 (т).