1. Главная
  2. ГДЗ
  3. 5 класс
  4. Математика
  5. Виленкин учебник
  6. 6.338. Часть 2

Задание 6.338 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2

Старая и новая редакции

Вернуться к содержанию учебника

6.335 6.336 6.337 6.338 6.339 6.340 6.341

Вопрос

Выберите год учебника

№6.338 учебника 2023-2024 (стр. 138):

Колибри легче воробья в 19,3 раза. Найдите массу каждой птицы, если колибри легче воробья на 31,11 г.

№6.338 учебника 2021-2022 (стр. 122):

Найдите значение выражения:

а) (143,65 - 40,7) : 2,9 - 17,75;

б) 8,74 : (2,43 + 2,17) - 0,475;

в) (21,2544 : 0,9 + 1,02 • 3,2) : 5,6;

г) 4,36 : (3,15 + 2,3) + (0,792 - 0,78)•350;

д) (3,91 : 2,3 • 5,4 - 4,03) • 2,4;

е) 6,93 : (0,028 + 0,36 • 4,2) - 3,5.

Подсказка

№6.338 учебника 2023-2024 (стр. 138):

Вспомните:

  1. Что называют уравнением, его корни.
  2. Умножение десятичных дробей (распределительное свойство).
  3. Деление десятичных дробей.
  4. Вычитание десятичных дробей.

№6.338 учебника 2021-2022 (стр. 122):

Вспомните:

  1. Порядок выполнения действий.
  2. Сложение и вычитание десятичных дробей.
  3. Умножение десятичных дробей.
  4. Деление десятичных дробей.

Ответ

№6.338 учебника 2023-2024 (стр. 138):

Пусть масса колибри г, тогда масса воробья 19,3 г. Известно, что колибри легче воробья на 31,11 г.

Составим уравнение:

19,3 - = 31,11

18,3 = 31,11

= 31,11 : 18,3

= 311,1 : 183

= 1,7

- 3 1 1 1     1 8 3              
1 8 3       1 7              
- 1 2 8 1                        
1 2 8 1                        
        0                        

1,7 г - масса колибри.

1,7 • 19,3 = 32,81 (г) - масса воробья.

  × 1 9 3
    1 7
+ 1 3 5 1
1 9 3  
  3 2 8 1

Ответ: колибри - 1,7 г, воробей - 32,81 г.

Пояснения:

Решаем задачу с помощью уравнения.

Пусть масса колибри г. Масса воробья в 1,4 раза больше массы колибри, тогда масса воробья 19,3 г. Известно, что колибри легче воробья на 31,11 г. Получается можем составить следующее уравнение:

19,3 - = 31,11.

В левой части полученного уравнения сначала применяем распределительное свойство умножения относительно вычитания (выносим за скобки), получим:

(19,3 - 1) = 31,11,

18,3 = 31,11.

Теперь находим неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:

= 31,11 : 18,3,

= 311,1 : 183,

= 1,7.

Учитывая обозначения введенные выше, масса колибри 1,7 г.

Масса воробья в 1,4 раза больше массы колибри, то есть масса воробья:

1,7 • 19,3 = 32,81 (г) .

Правила вычислений с десятичными дробями смотрите в подсказке.

№6.338 учебника 2021-2022 (стр. 122):

        •      
1) - 1 4 3 , 6 5
    4 0 , 7 0
    1 0 2 , 9 5
 
2) - 1 0 2 9 5     2 9  
    8 7         3 5 5
    - 1 5 9            
    1 4 5            
      - 1 4 5          
      1 4 5          
            0          
    • •   •  
3) - 3 5 , 5 0
  1 7 , 7 5
    1 7 , 7 5
 

1) + 2 , 4 3
  2 , 1 7
    4 , 6 0
2) - 8 7 4     4 6
  4 6       1 9
  - 4 1 4        
  4 1 4        
        0        
        • •  
3) - 1 , 9 0 0
  0 , 4 7 5
    1 , 4 2 5

1) - 2 1 2 5 4 4     9        
  1 8             2 3 6 1 6
    - 3 2                    
    2 7                    
      - 5 5                  
      5 4                  
        - 1 4                
          9                
          - 5 4              
          5 4              
              0              
2)   × 1 0 2
      3 2
  +   2 0 4
  3 0 6  
    3 2 6 4
3) + 2 3 , 6 1 6
    3 , 2 6 4
    2 6 , 8 8 0
4) - 2 6 8 8     5 6
  2 2 4       4 8
    - 4 4 8        
    4 4 8        
          0        

1) + 3 , 1 5
  2 , 3 0
    5 , 4 5
2) - 0 , 7 9 2
  0 , 7 8 0
    0 , 0 1 2
3) - 4 3 6       5 4 5  
  4 3 6 0     0 , 8  
          0            
4)   × 0 0 1 2  
        3 5 0
  +       6 0  
      3 6    
        4 2 0 0
5) + 0 , 8
  4 , 2
    5 , 0

1) - 3 9 1     2 3
  2 3       1 7
  - 1 6 1        
  1 6 1        
        0        
2)   × 1 7
    5 4
  +   6 8
  8 5  
    9 1 8
3) - 9 , 1 8
  4 , 0 3
    5 , 1 5
4)   ×   5 1 5
        2 4
  +   2 0 6 0
  1 0 3 0  
    1 2 3 6 0

1)   × 0 3 6
      4 2
  +     7 2
  1 4 4  
    1 5 1 2
2) + 0 , 0 2 8
  1 , 5 1 2
    1 , 5 4 0
3) - 6 9 3     1 5 4
  6 1 6     4 , 5
    - 7 7 0        
    7 7 0        
          0        
4) - 4 , 5
  3 , 5
    1 , 0

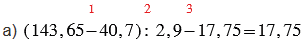
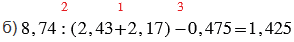
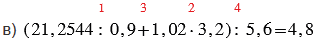
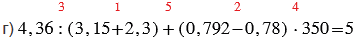
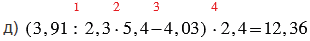
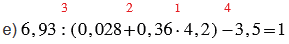
Пояснения:

Действиями первой ступени называют сложение и вычитание чисел, а действиями второй ступени - умножение и деление чисел.

При вычислении значений выражений порядок выполнения действий определяют следующие правила:

1. Если выражение содержит только действия одной ступени и в нем нет скобок, то действия выполняют по порядку слева направо.

2. Если в выражении нет скобок, то сначала выполняют действия второй ступени, потом - действия первой ступени.

3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая правила 1 и 2).

Красные числа, стоящие сверху над действиями, показывают в каком порядке нужно выполнять действия.

Правила вычислений с десятичными дробями смотрите в подсказке.

6.335 6.336 6.337 6.338 6.339 6.340 6.341

Вернуться к содержанию учебника