Задание 6.71 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2. Страница 86
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№6.71 учебника 2021-2022 (стр. 86):
Найдите корень уравнения:
а) 25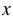
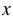- (14 + 8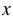) = 2427;
б) 23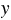
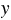- (25 - 11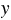) = 7245.
Подсказка
№6.71 учебника 2021-2022 (стр. 86):
Вспомните:
- Что называют уравнением, его корни.
- Умножение чисел, его свойства.
- Сложение чисел.
- Вычитание чисел.
- Деление чисел.
Ответ
№6.71 учебника 2021-2022 (стр. 86):
а) 25
- (14 + 8) = 2427
25 - 22 = 2427
3 = 2427
= 2427 : 3
= 809
| - | 2 | 4 | 2 | 7 | 3 | |||||||||||
| 2 | 4 | 8 | 0 | 9 | ||||||||||||
| - | 2 | 7 | ||||||||||||||
| 2 | 7 | |||||||||||||||
| 0 |
Ответ: = 809.
б) 23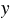
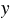- (25 - 11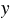) = 7245
23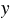 - 14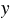 = 7245
9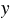 = 7245
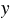= 7245 : 9
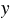= 805
| - | 7 | 2 | 4 | 5 | 9 | |||||||||||
| 7 | 2 | 8 | 0 | 5 | ||||||||||||
| - | 4 | 5 | ||||||||||||||
| 4 | 5 | |||||||||||||||
| 0 |
Ответ: 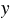= 805.
Пояснения:
а) В уравнении 25 - (14 + 8) = 2427 сначала выполняем вычисления в скобках, применяя распределительное свойство умножения относительно сложения (выносим за скобки и выполняем сложение в скобках), получим:
25 - (14 + 8) = 2427,
25 - 22 = 2427.
Теперь в левой части уравнения применяем распределительное свойство умножения относительно вычитания (выносим за скобки и выполняем вычитание в скобках), получим:
(25 - 22) = 2427,
3 = 2427.
В полученном уравнении неизвестен множитель , чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, получим:
= 2427 : 3,
= 809.
б) При решении уравнения
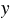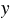23 - (25 - 11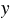) = 7245 действуем по алгоритму, приведенному в пункте а).
Вернуться к содержанию учебника