Задание 2.96 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.96 учебника 2023-2024 (стр. 56):
Найдите НОК(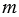
, 
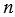), если:
а) 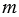= 2 • 3 • 3 • 5 • 11 и
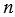= 2 • 2 • 3 • 3 • 3 • 11;
б) 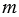= 2 • 3 • 5 • 5 и
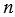= 2 • 3 • 3 • 5 • 5 • 7;
в) 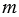= 2 • 2 • 5 • 5 • 13 и
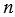= 2 • 2 • 2 • 3 • 5 • 13;
г) 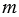= 2 • 2 • 5 • 5 • 17 и
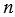= 2 • 2 • 3 • 5 • 5 • 17.
№2.96 учебника 2021-2022 (стр. 48):
Запишите в виде обыкновенной дроби числа 0,5; 0,24; 0,75.
Подсказка
№2.96 учебника 2023-2024 (стр. 56):
Вспомните:
- Как найти наименьшее общее кратное (НОК).
- Разложение на простые множители.
- Какие числа называют простыми.
- Умножение чисел.
№2.96 учебника 2021-2022 (стр. 48):
Ответ
№2.96 учебника 2023-2024 (стр. 56):
а)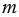 
= 2 • 3 • 3 • 5 • 11 и
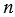= 2 • 2 • 3 • 3 • 3 • 11
НОК(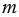; 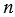) = 2 • 2 • 3 • 3 • 3 • 5 • 11 =
= 4 • 27 • 55 = 220 • 27 = 5940.
| × | 2 | 2 | 0 | |
| 2 | 7 | |||
| + | 1 | 5 | 4 | |
| 4 | 4 | |||
| 5 | 9 | 4 | 0 |
Ответ: НОК(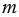; 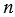) = 5940.
б) 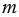= 2 • 3 • 5 • 5 и
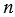= 2 • 3 • 3 • 5 • 5 • 7
НОК(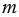; 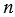) = 2 • 3 • 3 • 5 • 5 • 7 =
= 6 • 15 • 35 = 90 • 35 = 3150.
| × | 3 | 5 | |
| 9 | 0 | ||
| 3 | 1 | 5 | 0 |
Ответ: НОК(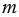; 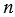) = 3150.
в) 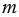= 2 • 2 • 5 • 5 • 13 и
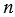= 2 • 2 • 2 • 3 • 5 • 13
НОК(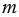; 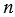) = 2 • 2 • 2 • 3 • 5 • 5 • 13 =
= 8 • 15 • 65 = 120 • 65 = 7800.
| × | 1 | 2 | 0 | |
| 6 | 5 | |||
| + | 6 | 0 | ||
| 7 | 2 | |||
| 7 | 8 | 0 | 0 |
Ответ: НОК(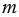; 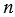) = 7800.
г) 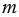= 2 • 2 • 5 • 5 • 17 и
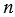= 2 • 2 • 3 • 5 • 5 • 17
НОК(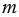; 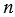) = 2 • 2 • 3 • 5 • 5 • 17 =
= 4 • 15 • 85 = 60 • 85 = 5100.
| × | 8 | 5 | |
| 6 | 0 | ||
| 5 | 1 | 0 | 0 |
Ответ: НОК(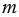; 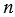) = 5100.
Пояснения:
Наименьшим общим кратным (НОК) нескольких натуральных чисел называют наименьшее натуральное число, которое делится на каждое из этих чисел.
Чтобы найти наименьшее общее кратное (НОК) нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители из разложения большего из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение этих множителей.
При выполнении умножения, опираясь на переместительное и сочетательное свойство умножения, группируем множители так как нам удобно (чтобы вычисления были проще).
№2.96 учебника 2021-2022 (стр. 48):
Вернуться к содержанию учебника