Задание 2.75 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.75 учебника 2023-2024 (стр. 53):
Существует ли четыре таких различных простых числа, что произведение двух из них равно произведению двух других?
№2.75 учебника 2021-2022 (стр. 46):
Определите, какими числами (простыми или составными) являются числа a, b и c на рисунке 37.

Подсказка
№2.75 учебника 2023-2024 (стр. 53):
Вспомните:
- Какие числа называют простыми и составными.
- Разложение на простые множители.
№2.75 учебника 2021-2022 (стр. 46):
Вспомните какие числа называют простыми и составными.
Ответ
№2.75 учебника 2023-2024 (стр. 53):
Таких чисел не существует.
Пояснения:
Произведение двух простых чисел - это составное число. Пусть a, b, c, d - различные простые числа. Запишем произвольные произведения пар этих чисел, например:
a•b, c•d.
Так как числа простые, то данные произведения являются разложениями чисел на простые множители, а так как любое составное число можно представить в виде простых множителей единственным способом, то a•b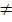 c•d, а следовательно, не существует четырех таких различных простых числа, что произведение двух из них равно произведению двух других.
c•d, а следовательно, не существует четырех таких различных простых числа, что произведение двух из них равно произведению двух других.
№2.75 учебника 2021-2022 (стр. 46):
а = 7•2 = 14 - составное число.
b = 7•3 = 21 - составное число.
с = 21•2 = 42 - составное число.
Ответ: все числа являются составными.
Пояснения:
Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число. Натуральное число называют составным, если оно имеет больше двух натуральных делителей.
С помощью линейки определим значения a, b, c:
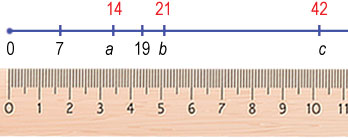
Числу 7 соответствует отрезок длинной 1,7 см, числу а соответствует отрезок 3,4 см, то есть число а в 2 раза больше 7, то есть:
а = 7•2 = 14.
Число 14 является составным, так как имеет больше 2 делителей. Аналогично получаем, что:
b = 7•3 = 21.
с = 21•2 = 42.
Данные числа также являются составными, то есть мы получили, что все числа являются составными.
Вернуться к содержанию учебника