Задание 3.142 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 146
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№3.142 учебника 2023-2024 (стр. 146):
№3.142 учебника 2021-2022 (стр. 146):
Масштаб карты 10 : 1 000 000. Заполните таблицу.
| Длина отрезка на карте | 3 см | 12 мм | |||
| Расстояние на местности | 10 км | 45 км | 1,5 км |
Подсказка
№3.142 учебника 2023-2024 (стр. 146):
№3.142 учебника 2021-2022 (стр. 146):
Вспомните:
- Что называют масштабом.
- Что называют пропорцией.
- Что называют уравнением, его корни.
- Умножение десятичных дробей.
- Деление десятичных дробей.
Ответ
№3.142 учебника 2023-2024 (стр. 146):
№3.142 учебника 2021-2022 (стр. 146):
| Длина отрезка на карте | 10 см | 3 см | 45 см |
1,5 см |
12 мм |
| Расстояние на местности | 10 км | 3 км | 45 км | 1,5 км | 1,2 км |
Масштаб:
10 : 1 000 000 = 1 : 100 000.
1) Длина отрезка на карте:  см,
см,
Расстояние на местности:
10 км = 10 000 м = 1 000 000 см.
 : 1 000 000 = 1 : 100 000
: 1 000 000 = 1 : 100 000
100 000 = 1 000 000
= 1 000 000
 = 1 000 000 : 100 000
= 1 000 000 : 100 000
 = 10 (см)
= 10 (см)
2) Длина отрезка на карте: 3 см,
Расстояние на местности:  см.
см.
3 :  = 1 : 100 000
= 1 : 100 000
 = 3 • 100 000
= 3 • 100 000
 = 300 000 (см)
= 300 000 (см)
300 000 см = 3000 м = 3 км
3) Длина отрезка на карте:  см,
см,
Расстояние на местности:
45 км = 45 000 м = 4 500 000 см.
 : 4 500 000 = 1 : 100 000
: 4 500 000 = 1 : 100 000
100 000 = 4 500 000
= 4 500 000
 = 4 500 000 : 100 000
= 4 500 000 : 100 000
 = 45 (см)
= 45 (см)
4) Длина отрезка на карте:  см,
см,
Расстояние на местности:
1,5 км = 1500 м = 150 000 см.
 : 150 000 = 1 : 100 000
: 150 000 = 1 : 100 000
100 000 = 150 000
= 150 000
 = 150 000 : 100 000
= 150 000 : 100 000
 = 1,5 (см)
= 1,5 (см)
5) Длина отрезка на карте: 12 мм,
Расстояние на местности:  мм.
мм.
12 :  = 1 : 100 000
= 1 : 100 000
 = 12 • 100 000
= 12 • 100 000
 = 1 200 000 (мм)
= 1 200 000 (мм)
1 200 000 мм = 1 200 м = 1,2 км
Пояснения:
Масштабом называют отношение длины отрезка на рисунке к длине соответствующего отрезка в реальности. Расстояние на местности и длина отрезка на плане должны быть выражены одинаковыми единицами измерения.
Частное 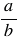 (
(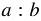 ) двух чисел
) двух чисел 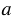 и
и  называют отношением этих чисел. Отношение показывает, во сколько раз число
называют отношением этих чисел. Отношение показывает, во сколько раз число 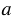 больше числа
больше числа  , или какую часть число
, или какую часть число 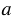 составляет от числа
составляет от числа  . Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю. Поэтому масштаб:
. Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю. Поэтому масштаб:
10 : 1 000 000 = 1 : 100 000.
1) Расстояние на местности 10 км или, учитывая то, что
1 км = 1000 м, а 1 м = 100 см, имеем
10 км = 10 000 м = 1 000 000 см.
Обозначаем длину отрезка на карте (в сантиметрах) буквой  и найдем отношение длины отрезка на карте к расстоянию на местности:
и найдем отношение длины отрезка на карте к расстоянию на местности:
 : 1 000 000.
: 1 000 000.
Оно будет равно масштабу карты:
1 : 100 000.
Значит,
 : 1 000 000 = 1 : 100 000.
: 1 000 000 = 1 : 100 000.
Чтобы найти неизвестный член полученной пропорции, используем основное свойство пропорции, согласно которому произведение крайних членов пропорции равно произведению ее средних членов, тогда:
100 000 = 1 000 000.
= 1 000 000.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
 = 1 000 000 : 100 000,
= 1 000 000 : 100 000,
 = 10.
= 10.
Значит, длина отрезка на карте равна 10 см.
2) Длина отрезка на местности 3 см. Обозначаем расстояние на местности (в сантиметрах) буквой  и найдем отношение длины отрезка на карте к расстоянию на местности: 3 :
и найдем отношение длины отрезка на карте к расстоянию на местности: 3 :  . Оно будет равно масштабу карты:
. Оно будет равно масштабу карты:
1 : 100 000.
Значит,
3 :  = 1 : 100 000.
= 1 : 100 000.
Чтобы найти неизвестный член полученной пропорции, используем основное свойство пропорции, согласно которому произведение крайних членов пропорции равно произведению ее средних членов, тогда:
 = 3 • 100 000,
= 3 • 100 000,
 = 300 000.
= 300 000.
Значит, расстояние на местности равно 300 000 см или, учитывая то, что
1 м = 100 см, а 1 км = 1000 м, имеем:
300 000 см = 3000 м = 3 км.
3) Рассуждаем аналогично пункту 1).
4) Рассуждаем аналогично пункту 1).
5) Рассуждаем аналогично пункту 2).
Вернуться к содержанию учебника